Introduction to Quaternions and Anatomical Movement Quaternions Provide a Language to Describe Movement If we are to talk about movements, we need a vocabulary and a syntax that allows us to speak precisely, clearly, efficiently and powerfully. It is the contention of this monograph that quaternion analysis provides such a language for describing anatomy and movement in three dimensions (Langer 2005a). A statement in such a descriptive language should have a precisely defined meaning that is accurately and clearly expressed. Each statement should correspond to a measurable or observable event or relationship. The terms and elements of the language must be unambiguous and there should be a minimum of unstated assumptions. A statement expressed in the language should include all the relevant points, but not be burdened with unnecessary detail. To that end, the vocabulary/symbolism must expand or contract to express the appropriate level of detail. Ideally, symbolic statements should express spatial relationships in an efficient format. The syntax of the language should contain much of the structure required by the task and the situation. Like Arabic numerals embed the rules of arithmetic in their organization, a descriptive language for movement should have the operations that are to be performed incorporated in its structure. The symbolic manipulation of the elements of the language should reflect the mechanics of the situation that is being described and yield new insights. If quantitative information is available, it should be possible to naturally embed the information in the descriptions of the anatomy and movements. The manipulation of the descriptions should flow from the syntax of the language. Quantitatively constructed statements should lead to equally quantitative and testable conclusions. Quaternions are a good choice for the description of rotations in three-dimensional space, because the multiplication of quaternions has the same formal structure as rotations of rigid bodies in three-dimensional space (Langer 2005b; Langer 2005c; Langer 2005d; Langer 2005e; Langer 2005f). In fact, one interpretation of quaternions is as the ratios of vectors in three-dimensional space (Hamilton and Joly 1869; Joly 1905; Kuipers 1999; Langer 2005d). The original motivation for HamiltonÕs invention of quaternions was to describe such rotations (Graves 1975). The ratio of any two three-dimensional vectors, a and b, may be expressed as a quaternion, . 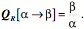
A quaternion can be written as a combination of a vector, which describes the axis of rotation, and a scalar that is a trigonometric function of the angular excursion of the rotation. Because of the geometrical directness of the relations between a quaternion and the rotation that it models, the use of quaternions is quite intuitive. With a bit of practice one can readily learn to write down the quaternion for a rotation directly from a mental image of the rotation. The intuitiveness of quaternions is one of the strongest reasons for using them. The formal structure of quaternions will be developed below. 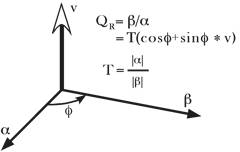
One interpretation of a quaternion is the ratio of two vectors. If two vectors, a and b, are translated so that they have common origin, then it is readily seen that the transformation of a into b may be expressed by specifying a unit vector perpendicular to the plane that they determine (v), the angle from a to b (), and the relative lengths of a and b (T). The quaternion that expresses the relationship is 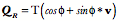 . . Nature of Anatomical Movement While quaternions may be applied to a wider range of movement than anatomical movements, we will consider their application to the types of movements that occur in animal bodies. Such movements will be called anatomical movements and they will generally be movements about joints. Movements about and within joints are typically rotations. Occasionally there will also be translation, but almost always in association with rotation. The advantage of rotation for anatomical movement is that there can be large excursions of body parts with comparatively small excursions within the joint itself. For instance, with movements in the gleno-humeral joint of the shoulder, the arm may move through more than 270¡ of angular excursion, a linear distance traveled by the hand is well over a meter, while the joint itself remains compact, with the humeral head always in contact with the small glenoid facet of the scapula, which is on the order of a centimeter across. The challenge of anatomical movements is that they occur in three dimensions. It is common to simplify the analysis of situations by constraining movements to two dimensions, but actual, natural, anatomical movements about a single joint are usually three-dimensional. They can, and often do, occur in more than one plane of rotation. A moving body part can trace a curved trajectory that is not confined to any single plane. Many anatomical movements are not naturally constrained to cardinal planes. Most involve both a swinging component and a torsional component (Standring 2005). Rotations in three dimensions are non-linear in the sense that the order in which they occur is relevant. Movement A followed by movement B will usually leave one in a different position than movement B followed by movement A. This can be readily seen by starting with your arm hanging at your side and the palm facing medially, then swinging your arm 90¡ about a horizontal axis, perpendicular to the sagittal plane, to bring it into a horizontal position, straight in front of your shoulder, and then 90¡ about a vertical axis to bring it straight lateral from your shoulder, with the palm facing forward. If we reverse the movements, the arm is first turned so that the palm is facing forward and then raised to straight in front of the shoulder with the palm facing up. The placement of your arm is clearly different, if the order of the rotations is reversed. Rotation of a bone about an axis of rotation that is not orthogonal to the axis of the bone, so that it traces out a conical surface, will create a concurrent axial torsion of the bone as it rotates. If your arm moves in a conical movement about a central axis, then it rotates about its long axis. Such concurrent rotations are a property of three-dimensional space and not particular to the bone or the joint except in the manner that the anatomy may constrain the movements of the bone. If we wish to describe such non-linear motions clearly and efficiently, we need a language that incorporates them naturally. It will be argued that quaternion analysis is just such a language. Compound Anatomical Movements Most natural anatomical movements are compound in the sense that they occur in more than one joint. The movements about each joint interact with those about the other joints to produce an aggregate movement that may be rather different from the component movements. Sometimes the aggregate movement may be quite simple while the components are complex. Watch as you reach for an object. The motion of your hand may be nearly a straight line between its starting point and its termination, but the movements around the joints in your shoulder, elbow, wrist and hand are all arcs, possibly in more than one plane. The relative movements in the individual joints are timed and paced so that the aggregate movement is straight and smooth. Your ability to coordinate all those movements so well, moment to moment, without considerable prior calculation, is actually a small miracle. If you were to have to program a machine to perform the same action, you would discover that it requires a massive calculation. Once again, we require a conceptual framework and notation that would simplify such calculations and quaternions prove to be such a framework. Orientation If you are reaching for a cup, then it is not sufficient that your hand move into the vicinity of the cup. It must also be properly oriented to grasp the cup. This requirement introduces a concept that is often ignored in the analysis of anatomical movements or implicitly assumed, but not explicitly dealt with. Orientation is an essential component of the movement. Anatomical objects are orientable. They have a top and bottom, a front and back, and a right and left side and, unless they are symmetrical, like a featureless sphere or a cylinder, you can tell how they are oriented in space. For instance, you can say how a hand is oriented in space. Furthermore, how structures are oriented is important. In anatomical movements, orientation is central to the movement. It cannot be ignored without loosing a great deal of information about the movement. If we are to talk about anatomical movements, we must talk about orientation. Right-handed versus Left-handed 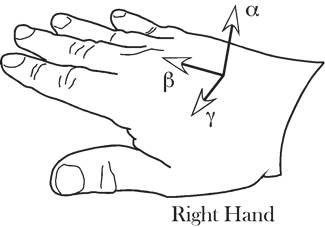
The orientation of a hand, or any other anatomical object, can be abstracted by attaching a set of reference vectors to the hand. In the case of a hand a convenient set of vectors might be a vector directed away from the plane of the hand, one in the direction of its longitudinal axis, and one in the direction of the thumb. If these vectors are constructed for the left hand, there is no way that you can rotate the set of vectors for the right hand to align with the set for the left hand, just as there is no way to make your right hand look like your left hand except by reflecting it in a mirror. You can tell a left hand from a right hand because the spatial arrangement of the fingers, thumb and palm are different. The three dimensional world in which we live and move allows for only two options, a left hand and a right hand, but it is not possible to turn one into the other unless you can turn the hand inside out. For instance, you can wear the glove for your right hand on your left hand if you turn it inside out. Flesh and blood hands cannot be inverted in the same manner, without an additional dimension. Because of the property of space that mandates left and right hands, it is also possible to specify the orientation of a hand in space. We can abstract the orientation of a hand by choosing three independent vectors relative to the hand. Let the first be directed dorsal to the hand (a), the second be in the direction of the middle finger (b), and the third be in the direction of the thumb (g). It simplifies analysis if the three vectors are mutually orthogonal, but it is not strictly necessary. The set of vectors for the right hand cannot be transformed into the set for the left hand by any combination of rotations or translations. If we allow mirror reflections then each is the reflection of the other. A set of unit vectors that specify the orientation of an anatomical structure will be called a frame of reference. They are attached to the object in the sense that as the object moves, they move, but they do not have a specific location. A frame of reference is an ordered set of directions. Right and Left-handed Coordinates 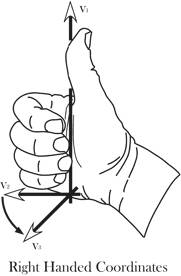
In a right-handed coordinate system, if your right thumb is aligned with one axis, then the fingers of your right hand curl in the direction that carries the next axis into the final axis. Assume a coordinate system in which one vector (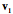 ) points away from the center of the earth, a second ( ) points away from the center of the earth, a second (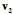 ) points east, and a third ( ) points east, and a third (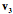 ) points north. Let us order them so that, if your right thumb is pointing in the direction of the first vector, then your curled fingers point in the direction that carries the second vector into alignment with the third vector. Any cyclic permutation of the vectors, ) points north. Let us order them so that, if your right thumb is pointing in the direction of the first vector, then your curled fingers point in the direction that carries the second vector into alignment with the third vector. Any cyclic permutation of the vectors, (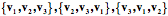 ), ), has that property. Such a system is said to be right-handed. Just as there are right and left hands, there are right and left–handed coordinate systems. For a left-handed coordinate system one would use oneÕs left hand to determine the order of the coordinates. Any permutation in which two of the vectors for right-handed system are exchanged will yield a left-handed coordinate system and vice versa. (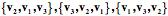 ). ). It does not matter which handedness you choose, but, having chosen, you must stay with that convention. Right-handed coordinates will be used here, unless specified otherwise. Location Location is a fundamental property of an object. It is a description of where it is in space. In order to specify a location one must have point of reference, which will called an origin, and a coordinate system that allows one to specify the extent to which the object lies in various directions. While not strictly necessary, it is convenient to have the coordinates of the space be a set of mutually orthogonal axes. It is also convenient that the three vectors be unit vectors, that is, that they have a length of 1.0. Such a set of vectors, that defines a space, is called its basis. It is essential that the three basis vectors be independent, meaning that no basis vector can be expressed as a combination of the other two vectors. Given an origin and a coordinate system built on a basis for that space, location can be specified as a combination of the basis vectors. A location vector, L, extends from some reference point, usually the origin, to the structure of interest. Location vectors are like the vectors that are generally encountered in physics in that they have direction and magnitude. However, there is also an implied null location or origin of the coordinate system, O. Such vectors are sometimes called fixed vectors. For reasons that will become apparent as we progress, let us call the unit basis vectors in the universal coordinate system i, j, and k. Also, for simplicity, let the coordinates for location be parallel to the universal coordinates, but to indicate that they are different from the universal coordinates let them be called x, y, and z. Then we can write the location, L, in terms of those coordinates. 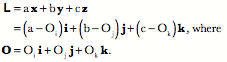
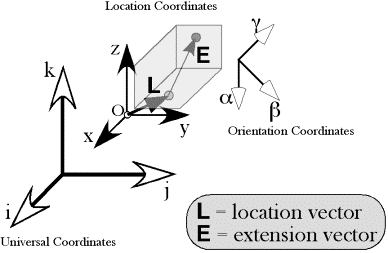
Extension and Orientation We can specify the extension of a hand in space by a three-dimensional vector that points from the center of the hand towards the base of the thumb, or the little finger, or to the dorsum or palm of the hand. Such vectors will be called extension vectors, because they express the extension of the hand in space. All of its extension vectors move with the hand. Extension vectors may be of any length and direction. With some thought, it becomes apparent that extension vectors also require a three-dimensional coordinate system. Extension vectors imply an origin, normally a point within the structure for which they are an extension. Also, just as the location vector implies a coordinate system in which the location of a hand is embedded, an orientation vector implies a coordinate system that travels with the hand. It is convenient to make the coordinate system the frame of reference for the structure, but it is not strictly necessary to do so. However, any coordinate system chosen can be expressed as a rotation of the orientation frame of reference, therefore, there is no loss in generality if we assume that the extension vectors are written as combinations of the frame of reference vectors. Both location vectors and extension vectors can be expressed in terms of the universal coordinate system; however, the coordinates for orientation are not located in the space for location. In fact, orientation vectors do not have location, only magnitude and direction. In the above illustration, the location coordinates {x, y, z} are mutually orthogonal unit vectors with a definite location in space, all taking origin from the point O. The orientation coordinates {a, b, g} are drawn at a particular location, because they have to be drawn somewhere, but any other location would be equally valid. The vectors need not have a common origin. It just makes it easier to appreciate their orientation if they occur together. Extension vectors do require a point of reference. It is usually convenient to make that point of reference, the location of the anatomical structure. However, any other point may be chosen, by creating the extension vector from the location of the object to the center for the extension vector(s). The new extension vector is the extension vector relative to the location of the object minus the offset vector for the point of reference for the extension vector. 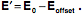
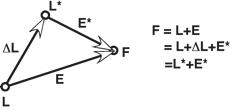
Extension depends upon location, but it transforms like orientation. The null location is arbitrary (L*), but it can always be referenced to the location of the object for which it is an extension (L). Orientability Extension vectors differ from location vectors in that they are orientable. Location vectors can be orientable, but it is not a part of their function. Let us consider what we mean by a vector being orientable. Orientability is an intrinsic property of quaternion vectors. It sets them apart from vectors normally encountered in vector analysis, although cross or vector products do retain elements of the orientability of quaternion vectors. Because of their orientability, quaternion vectors are a natural way to express orientation. In quaternion analysis, a vector may be interpreted as the ratio of two orthogonal vectors in the plane perpendicular to the vector. In the example sketched below, the quaternion vector g implies the vectors a and b. They are part of the vector, 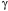 ; g is the ratio of b to a. ; g is the ratio of b to a. 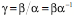 . .
Actually, the a and b vectors can be any two mutually perpendicular vectors in the plane perpendicular to g such that a turns into b about the positive g direction and the ratio of the length of b to the length of a is the length of the vector g, that is a, b, and g form a right handed coordinate system. The quaternion vector g may be viewed as the vector g and/or as the plane that is perpendicular to g. The vectors a and b lie in that plane and define it. The vector g does not select a particular a and b. The orientation of the plane is definite and unique, but it has no particular location. 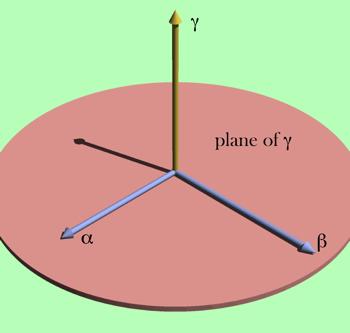
The vector g is equivalent to the oriented plane that lies perpendicular to it and it may be defined as the ratio of two perpendicular vectors in that plane. For many purposes, it is convenient to choose a particular set of vectors that encapsulate an orientation. We pick a particular set of unit vectors, a, b, and g, , respectively, that are related so that that each is the ordered product of the other two ( ). Orientation is about how those vectors are transformed by movements. Such a set of vectors is a frame of reference. ). Orientation is about how those vectors are transformed by movements. Such a set of vectors is a frame of reference. Expressing Extension in Terms of Orientation Consider an example. To specify the orientation of the hand, we need three vectors, which we can choose as we want, but, again for simplicity, let us choose the first vector to be perpendicular to the dorsal surface of the hand (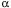 ), the second vector pointing in the direction of the middle finger ( ), the second vector pointing in the direction of the middle finger (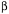 ), and the third vector pointing towards the thumb ( ), and the third vector pointing towards the thumb (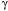 ). Also, let a, b, and g all be unit vectors, that is, let them have a length of 1.0. These three basis vectors specify a frame of reference for the orientation of the hand. ). Also, let a, b, and g all be unit vectors, that is, let them have a length of 1.0. These three basis vectors specify a frame of reference for the orientation of the hand. To specify a point on the hand, E, in the local coordinate system for the hand, we can write it as a linear combination of the three orientation vectors, 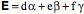 . The vector E is an extension vector. Extension vectors are useful for describing the anatomy of a body part, because they specify the locations of its components relative to the body part. In rigid objects, the relations between extension vectors are constant. . The vector E is an extension vector. Extension vectors are useful for describing the anatomy of a body part, because they specify the locations of its components relative to the body part. In rigid objects, the relations between extension vectors are constant. 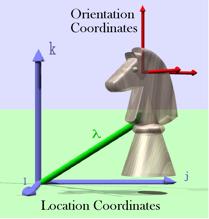
The placement of the knight is determined by its location (l) and orientation. Its shape and the relative locations of its parts may be expressed by a collection of extension vectors. Its location coordinates were chosen to be aligned with the universal coordinates (i, j, k). Its orientation coordinates may also be expressed in the same coordinates. However, the two coordinate systems are independent. Let us use the term placement to indicate the combination of location and orientation of the hand. Given its location and orientation, we know how it is situated in space. Placement, P, is a given by location (L) and orientation (f), each of which has its own coordinate system. The extension vector is orientable and it depends upon both orientation and location. 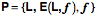
Degrees of Freedom The location and extension vectors of placement have three coefficients each, so placement has six coefficients, thus there are six degrees of freedom when describing an anatomical object. The description of anatomical placement requires six degrees of freedom for every moving component. To return briefly to the reaching problem that started this discussion, assuming that your trunk is stationary, there are movements of your scapula upon your trunk, your humerus upon your scapula, your ulna upon your humerus, your radius upon your ulna, and your wrist upon your radius. Consequently, the linkages responsible for the placement of your hand have 30 degrees of freedom. Clearly, the control of movement can be complex. Your hand has six degrees of freedom for its placement, so the many degrees of freedom for the joints that move the hand reduce to many fewer degrees of freedom though internal relationships among the descriptions of the joints. The addition of the three degrees of freedom for orientation has anatomical consequences. In order to control movements about a joint, one must have at least the same number of independent movers as there are degrees of freedom. That is not to say that a muscle need pull in a cardinal direction or even that a muscle need have a consistent direction of action. Clearly muscles may change their role depending upon the configuration of the joint and the distribution of muscles about the joint. This problem will be considered below, when we examine the role of the extrinsic eye muscles in the movements of the eyeball. Movement Transforms Descriptions of an Anatomical Object Movement usually changes location. To describe a movement of an anatomical object one needs to specify its location before and after the movement. One might conceivably want follow more than one location, such as, the proximal and distal ends of the humerus, however, that information is usually more efficiently encoded as vectors that extend from a single location for the object. Computing a change in location with rotation is generally a more complex operation that computing a change in extension (see below). Rotation changes extension. It is often convenient to generate an image of the moving object and indicate how movement changes that image. The image is expressed as one or more extension vectors. Transformations of images of objects become important in descriptions of multi-joint movements in which the location of the joints change as a consequence of the movement. For instance, if describing movements of the arm and forearm, the movements of the arm in the gleno-humeral joint will cause the elbow joint to move. A minimal description of the humerus in such an analysis would indicate where the distal joints of the humerus are located relative to the location of the humerus. Transformations of images of an object also become important when the image is complex, reflecting multiple features of the anatomical object. For example one might wish to track the movements of the articular faces of a vertebral body, the facet joints, and the spine of a vertebra. In such a situation, there will be multiple extension vectors. Finally, rotation changes orientation. Translation does not change the orientation of an object. That is in effect the definition of translation, a movement that does not change orientation. Unless the rotation is a complete circle in a single plane, rotation always changes orientation. Because extension may be expressed as a combination of orientation vectors, rotation also transforms extension. Frames of Reference To characterize orientation, we need a set of three vectors that express the orientation of the object. We call such a set of vectors a frame of reference. The convention will be to choose three mutually orthogonal unit vectors that form a right–handed coordinate system. Where the meaning is obvious, frames of reference will be called simply frames. Transformations of frames is central to most of what follows. Framed Vectors and their Transformations by Movements To capture an anatomical motion, we often need a location for the body part, the extension of one or more components of the body part, and the orientation of the body part. These are expressed as a location vector, extension vectors, and a frame of reference, respectively. Together, these vectors constitute a framed vector. Each component of a framed vector is transformed differently by motion. We will use framed vectors to describe anatomical objects. A framed vector is actually a set of vectors. By convention, the first vector in the set will be the location of the object. The second vector will be an extension vector that describes a relevant morphological locus in or on the object, relative to the location of the object. There may be many extension vectors, since it may be relevant to express the locations of multiple loci relative to the object. The last component of the framed vector is a set of three mutually orthogonal unit vectors that specify an orientation for the object, that is, a frame of reference. Consequently, a complete framed vector has a minimum of five vectors, a location vector, an extension vector, and three frame of reference vectors. It may have more than one location vector or more than one frame of reference, but there are more efficient ways of encoding that information. A framed vector may have, and often will have, many extension vectors, to describe an object. The numbers of extension vectors is the most variable feature of framed vectors. In some instances, if we are primarily interested in the orientation of the object, the location vector may be the origin and the extension vectors may be stripped, in which case the framed vector may be only a frame of reference. Framed vectors are a very flexible concept. Basically, they are a description of an object. Consequently any description expressed as a combination of location, extension and/or orientation will fall within the definition of a framed vector. They are useful concepts, because movement transforms their components in standard ways. Location is changed by both translation and rotation. Location says where an object is in space by choosing one point to represent the entire object. For the hand, we might designate the center of the middle carpal-metacarpal joint as its location, so that the location of that point is the location of the hand. A translation is a movement that moves an object without changing its orientation. Translations change an objectÕs location. Lifting your hand straight up from the table is a translation. A rotation is a movement about an axis of rotation and it generally changes the orientation of the moving part. Bending your elbow is a rotation that changes the orientation of your hand. Rotations will not change the location of an object if their axis of rotation contains the point that is considered the location of the object. Otherwise rotation changes location. In many situations, we are interested in how a part of an anatomical object moves, say the distal end of the third metacarpal so we create an extension vector that represents the offset of the distal end of the third metacarpal relative to the proximal end. In some situations, there may be an array of points that are of interest. For instance, if we are examining the movements of a vertebra, it may be of interest to know where the superior and inferior surfaces of the vertebral body lie and where the facets are located. If we have an array of extension vectors defined relative to the center location of the vertebra, then we can compute the new array by applying the same transformation to all the points in the array as it existed prior to movement. Unlike location, extension is not changed by translation, because extension is measured relative to a point upon or within the moving object. Rotation always changes extension. Consequently, extension does not transform like location, even though it is the difference between two locations. If expressed in location coordinates, the transformation of extension vectors is complicated. One must move the object so that the center of the object is located on the axis of rotation, the rotation transform is then applied to the extension vector, and then the rotated extension vector is translated back to its original location. If expressed as combinations of the frame of reference vectors, then the calculation of the change in extension requires only that the new values of the frame of reference vectors be substituted into the extension vectors. The new extension vectors are added to the new location to obtain the new locations of the points described by the extension vectors. Finally, we need at least one frame of reference. In a rigid body, one frame of reference is sufficient, because any other frame can be expressed as a rotation transformation of that frame. It is simply a matter of taking the ratio of the two frames, to obtain the rotation that transforms one into the other. A means of computing the ratio of two frames of reference will be developed below. By the definitions of translation and rotation, orientation is changed by rotation, but not translation. Consequently, orientation is like extension in the types of movements that transform its frame of reference. Unlike extension, orientation does not interact with location although it can depend upon location and can determine where loci on the anatomical object end up being located. The component axes of the frame of reference might be viewed as a set of unit extension vectors, but orientation is not tied to location. A frame of reference may be drawn near a point on the anatomical object as a convenience, but orientation is not attached to any particular part of the object. It is a property of the object as a whole. Even though it may be expressed in the same coordinate system as the location and extension vectors, orientation is, in effect, a different space. It does not make physical sense to combine location and orientation by adding one to the other or multiplying them, because they are different, independent spaces. Location does not have orientation and orientation does not have location. Rotation We have gone to some considerable trouble to describe the location, shape, and orientation of an anatomical object. This was all to provide a foundation for the description of movements of that object. Now let us consider how movement may be described. The movements of primary interest here are rotations. Such movements occur about an axis of rotation and through an angular excursion. It turns out that if we express the axis of rotation as a unit vector aligned with the axis of rotation, v, and the angular excursion as an angle, f, then the rotation may be expressed as a quaternion. 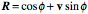
If a vector, s, is rotated about the axis of rotation as indicated by the quaternion R, then the new value of the vector, 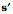 , is given by the following expression. , is given by the following expression. 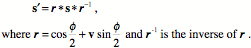
There is some background work to be done, like what an inverse of a quaternion might be and how one multiplies quaternions, but this relationship expresses the essence of rotations of orientable objects. In the next section we will consider the nature of quaternions in some depth and briefly introduce some of the principles of quaternion analysis. Graves, R. P. (1975). Life of Sir William Rowan Hamilton. New York, Arno Press. Hamilton, W. R. and C. J. Joly (1869). Elements of quaternions. New York,, Chelsea Pub. Co. Joly, C. J. (1905). A Manual of Quaternions. London, Macmillan and Co. Ltd. Kapandji, I. A. (1974). The Physiology of the Joints. Annotated diagrams of the mechanics of the human joints. New York, Churchill Livingstone. Kuipers, J. B. (1999). Quaternions and Rotation Sequences: A Primer with Applications. Princeton, New Jersey, Princeton University Press. Langer, T. P. (2005a). Geometrical Anatomy?: http://homepage.mac.com/tlanger_sasktel_net/GeometricalAnatomy.html. Langer, T. P. (2005b). Modeling Rotations of Orientable Objects in Three Dimensions: An Introduction to Quaternions and Framed Vectors.: http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html. Langer, T. P. (2005c). Geometrical Anatomy and Anatomical Movements: An Introduction to the Use of Quaternions and Framed Vectors in the Description of Anatomical Rotations. : http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html. Langer, T. P. (2005d). Commentary on JolyÕs Manual of Quaternions: http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html. Langer, T. P. (2005e). Structural Ratios: The Comparison of Structures and Their Parts.: http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html. Langer, T. P. (2005f). The Geometrical Anatomy of Compound Movements.: http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html. MacConaill, M. A. (1964). "Joint movements." Physiotherapy(November): 359-367. MacConaill, M. A. (1966). "The geometry and algebra of articular kinematics." Bio-Med Eng 1: 205-212. MacConaill, M. A. and J. V. Basmajian (1977). Muscles and Movements. A basis for human kinesiology. . New York, Krieger. Standring, S. (2005). Gray's Anatomy. The Anatomical Basis of Clinical Practice. Edinburgh, Elsevier Churchill Livingstone. Stewart, I. (2007). Why Beauty is Truth. A History of Symmetry. New York, Basic Books. |