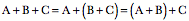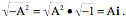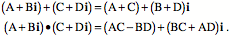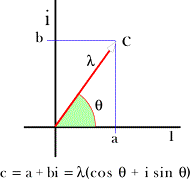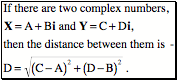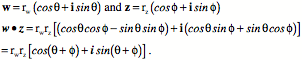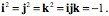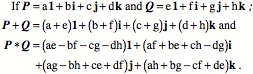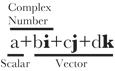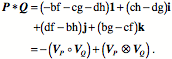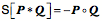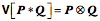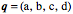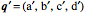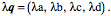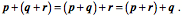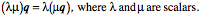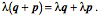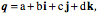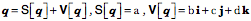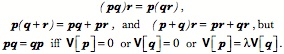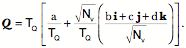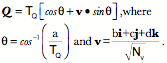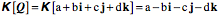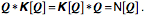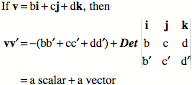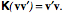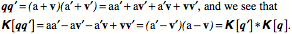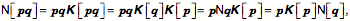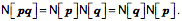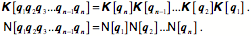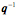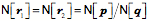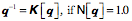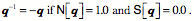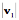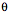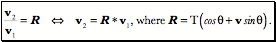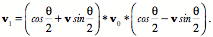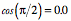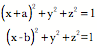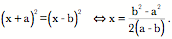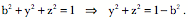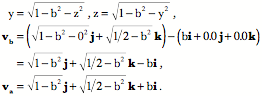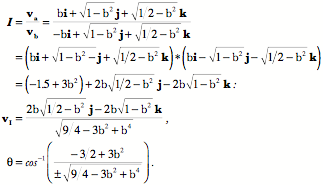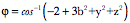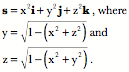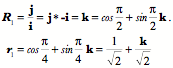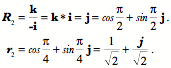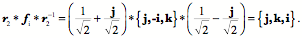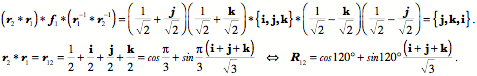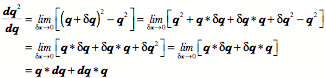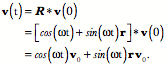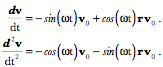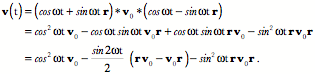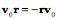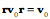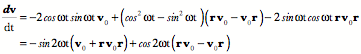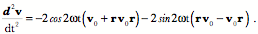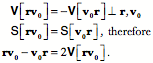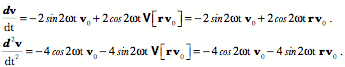Quaternion Numbers

To this point, we have used quaternions as a means to an end, the description of anatomical movement. Along the way, we have introduced a number of attributes of quaternions, but not considered quaternions as entities in themselves. They are interesting in themselves, as mathematical objects. In this section, we will consider some of the mathematical properties of quaternions.

We will build up the quaternions from simpler number systems. Since our objective is to understand quaternions, much of the material on the other numbers will be briefly covered. There are many excellent books that cover this initial material in much more detail. Many of the points raised here can be explored greater depth in a recent book by Ian Stewart (Stewart 2007).

Rational Numbers

Quaternions are a natural extension of the types of numbers that one is apt to be conversant with (Langer 2005e). Perhaps the simplest numerical structures are the counting numbers (1, 2, 3…), which are extended by the addition of the negative numbers and zero to form the integers. The integers are an improvement upon the counting numbers because they are closed over addition, subtraction, and multiplication. That means that one can add, subtract, or multiply any two integers and the result is an integer. To obtain closure under division it was necessary to add fractions, to obtain the rational numbers. Rational numbers can be expressed as the ratio of integers.

The counting numbers are useful for measuring the numbers of elements in a group, such as the number of sheep in a pen. They can be used for rudimentary measuring of the length or volume of something, such as the number of buckets of water needed to fill a tank. However, if one wants any degree of precision it is necessary to develop fractions of the basic unit of measurement, such as 2 meters, 2 centimeters, and 3 millimeters of length or 60 degrees, 10 minutes and 21 seconds of angular excursion.

Properties of rational numbers

For all practical measurements, the rational numbers are adequate. Mathematically, they make a closed system of numbers that are self-contained in the sense that all four arithmetical operations operating upon them yield other members of the group. It also turns out that the order in which you add or multiply them is irrelevant to the final outcome, , and , which is to say that they are commutative. When more than two numbers are added or subtracted they may be grouped as is convenient without changing the final result, and , which is the associative property. Combined addition and multiplication, , are distributive.

There are additive and multiplicative identities, that is, elements of the number system that do not change the value of a number if added to it or if multiplied by the identity, and . There is an additive inverse for each rational number, that is, a number that added to an integer will give zero as a final result, . Because division by any non-zero rational number is allowed there is a multiplicative inverse for each rational number ().

Finally, the rational numbers are ordered. It is possible to place them in a sequence that progresses from the smallest to the largest and any rational number can be placed between two other rational numbers. In addition, it can be shown that between any two rational numbers, no matter how close they lie to each other there is at least one more rational number. Because of these attributes all the rational numbers can be represented as points on a line and the density of the points can be made as dense as you desire. Such a line is called a rational number line. It is an intuitive geometrical representation of the rational numbers. Mathematical operations using the rational numbers can be represented by constructions performed upon the rational number line.

Irrational numbers

As a consequence of these properties, the rational numbers form a very elegant closed system of numbers that seem to work for all practical measurements. It came as a great shock to the early Greek mathematicians to discover that there a many numbers that lie amongst the rational numbers that cannot be expressed as a fraction. For instance, the diagonal of a right triangle with unit length sides has a length that cannot be expressed as a rational number. By the Pythagorean theorem, the square of the length of the hypotenuse is equal to the sum of the squares of the sides of a right triangle. However, it is fairly readily demonstrated that there is no fraction that exactly equals the .

Probably because they did not make sense in the context of the current mathematics, such numbers were called irrational numbers. They are in fact no more reasonable and no less reasonable than rational numbers, just unexpected. It turns out that they are essential for certain types of mathematics that we use to run our everyday world.

There are many more irrational numbers than there are rational numbers. It is possible to show that there are as many rational numbers as there are positive integers, that is, a countable infinity. One can put the rational numbers in a one-to-one relationship with the integers, consequently, there are the same number of rational numbers as there are integers. However, there are infinitely many times as many irrational numbers, that is, an uncountable infinity. That is because there is no way to place the irrational numbers in one-to-one association with the integers. In fact for every rational number, there is an uncountable infinity of irrational numbers.

Real numbers

If we combine the irrational numbers and the rational numbers, the number system is called the real numbers. Real numbers have all the properties that we associate with rational numbers. In addition they account for every point on a number line, allowing some mathematics that is not possible with rational numbers, because they form a continuum. That property of real numbers makes them the natural basis for calculus and analysis, where one examines relationships as the scale of examination smoothly approaches zero width on the number line.

Complex numbers

Like the hypotenuse of a right triangle, there turned out to be other simple mathematical problems that led to inconvenient numbers, which were not real numbers. For instance, the solution for the roots of certain cubic equations leads to perfectly acceptable real roots, but only if one acknowledges that there are square roots of negative numbers. There are no such numbers in the set of real numbers, because the product of two negative real numbers is a positive real number and the product of two positive real numbers is a positive real number. Since the square root of a negative number can be expressed as the product of the square root of the positive real number and the square root of -1, if the has meaning, then the square root of the negative number has meaning.

There was considerable agonizing over the meaning of , but eventually it was decided that one could treat it as a perfectly reasonable number, so it was symbolized by i (sometimes by j in some engineering applications). Again, because it did not fit in the general concept of numbers, such numbers as were called imaginary numbers. It is perfectly natural to combine real numbers and imaginary numbers or form a two part number that was called a complex number,. Complex numbers obey all the rules of algebra if we remember that . It follows that –

Addition simply adds the real components and the imaginary components of the complex numbers. Multiplication depends upon combinations of the real and imaginary components, but it is simply algebraic multiplication.

A complex number may be written as the sum of a real number, a1, and an imaginary number, bi. It may also be written as a trigonometric expression.

We can extend our geometrical representation of the real numbers by drawing a line perpendicular to the real number line and placing the imaginary numbers along that line so that the zero on both lines is the same. Then, the complex numbers are constructed by going along the real number line to the value of the real component and then along a line parallel with the imaginary number line a distance equal to the real part of the imaginary number.

Notice that the imaginary numbers are not closed under multiplication, because the product of two imaginary numbers is a real number. However, the complex numbers are closed under addition and multiplication, they are commutative, associative, and distributive, and they have additive and multiplicative identities and inverses. On the other hand, they are not ordered. It does not make sense to say that one complex number is greater or lesser than another.

Notice that it does make sense to say to say that one complex number is closer to a given complex number than another is. One simply has to define distance in the complex number plane.

The length of the vector that extends from the origin to a complex number is the magnitude of the complex number. The length squared is called the norm of the complex number.

Otherwise, complex numbers have all the nice properties of real numbers, so they are an excellent basis for analysis and it turns out that many problems in analysis are more readily treated and deeply understood in complex analysis.

One of the nice properties of complex numbers is that they can be interpreted as rotation in the complex plane. To see that, one needs to express the complex numbers in a different, but equivalent, form. First, note that the complex number is in rectangular coordinates, but it might equally well be expressed in polar coordinates as , where r and q are given by . The norm of the complex number is ‘’ and the angle is q. That may not seem like much of an improvement, but consider what happens when we perform multiplication.

The product of two complex numbers is the product of their magnitudes and the sum of their angles. If one of them, say w, is a unitary complex number (), then the product is the rotation of z about the origin through an angular excursion of q. This feature of complex numbers is a very useful property for many types of applications of complex numbers, especially several branches of physics. Once again, a strange type of number that seems to be a mathematical curiosity turns out to be a very useful tool for understanding the real world.

Quaternions

In the mid eighteen hundreds William Rowan Hamilton was looking for a way to extend the complex numbers to three dimensions. He was looking for a way to express rotations similarly in three-dimensional space. Logically, since complex numbers have two components and they describe rotations in two-dimensional spaces, would one expect it to take three components to describe rotations in three-dimensional space? In retrospect, the answer is obviously no. It takes more information than can be contained in three real numbers. It takes three coordinates to specify a direction, an axis of rotation, and one to specify the angular excursion of the rotation. The answer turned out to be a number with four components that combine in special ways. The answer turned out to be quaternions.

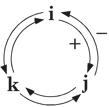
A quaternion may be viewed as the ratio of two vectors. It may be written as the sum of four types of number, a real number or scalar, and three different imaginary numbers (i, j, k). It may also be written in a trigonometric format.

Quaternions are ordered collections of four real numbers, which is the basis for their name. One of the components is a real number, called a scalar, much like the real term in a complex number. It may be thought of as a multiple of unity. The other three components form a vector. Each component of the vector is multiplied by a different imaginary number, i, j, or k. The numbers i, j, and k are imaginary numbers because their squares are equal to -1. They are different imaginary numbers because the product of any two of them is plus or minus the third. That is summarized in the following expression.

It took years for Hamilton, one of the greatest mathematicians of all time, to discover the quaternions, largely because it was necessary to violate one of the cardinal rules in all known algebras of the time. In quaternion algebra, multiplication is not commutative, . That property of quaternions is embedded in the system by the rule that multiplying the imaginary components gives the positive of the third if they are multiplied in the order and the negative of the third if they are multiplied in the opposite order, . Consequently, , but.

Multiplication of two imaginary numbers in a clockwise order gives the positive value of the third imaginary number. Multiplication in a counter-clockwise direction gives the negative value. Multiplication of an imaginary number by itself yields -1.

Other than the rule about the multiplication of the imaginary components, the algebra of quaternions is algebraic in the same ways as apply to real and complex numbers. When adding quaternions, the coefficients of each component are added together. In multiplication, the coefficients interact in an intricate, but logical, manner.

Note that the complex numbers are a subset of the quaternions. If we set two of the imaginary coefficients equal to zero then the formulas are the same as for complex numbers. If we set all the coefficients of the imaginary terms equal to zero then the quaternions are the real numbers. If we set the scalar components equal to zero, then we have vectors. Vectors were originally described in quaternion analysis and subsequently reinterpreted in vector analysis.

A quaternion may be viewed as the combination of a real number or scalar and a vector. The vector is the sum of three different imaginary numbers. The scalar plus one of the imaginary numbers is a complex number. Consequently, the real and complex numbers are subsets of the quaternions.

Multiplication of Vectors

Quaternion vectors are different from the vectors in vector analysis in the way that they combine in multiplication. When we multiply quaternion vectors, we do not get the usual dot product or the cross product of vector analysis, but a combination of both.

The dot product (scalar product, inner product) and cross-product (vector product, outer product) were first defined in quaternion analysis, but subsequently slightly redefined when the concepts were incorporated into vector analysis. In this book, we usually refer to the scalar of the product, , and the vector of the product, , rather then the terms used elsewhere. Unlike vector analysis, there is only one type of multiplication in quaternion analysis and it yields quaternions with both a scalar component and a vector component.

Quaternions are closed under division

Division of vectors has no meaning in vector analysis unless the vectors are parallel or anti-parallel. If two vectors point in the same or opposite directions, then one is a scalar multiple of the other. The ratio is a real number or scalar. Otherwise, the ratio of two vectors is nonsense.

The ratio of two vectors is one of the most useful operations in quaternion analysis. Any vector, in fact, any quaternion may be divided by any other vector or quaternion, unless the object in the denominator is zero. Because that is true of quaternions, the quaternions form a complete, non-orderable, division algebra.

There are only four division algebras, the real numbers (1 component), the complex numbers (2 components), the quaternions (4 components), and octonions (8 components). Octonions are an extension of quaternions with eight components, which are not commutative for multiplication (like quaternions) and not associative for multiplication, . They may also be called Cayley numbers. Until quite recently, octonions were largely a mathematical curiosity, but it is beginning to look like they might be critical to an understanding of the fundamental structure of space and time in theories like superstring theory (Conway and Smith 2003; Stewart 2007).

The following quote expresses the general attitude towards quaternions and octonions. The real numbers are the dependable breadwinner of the family, the complete ordered field we all rely on. The complex numbers are a slightly flashier but still respectable younger brother: not ordered, but algebraically complete. The quaternions, being noncommutative, are the eccentric cousin who is shunned at important family gatherings. But the octonions are the crazy old uncle nobody lets out of the attic: they are nonassociative. — John Baez (Baez 2002)

Quaternions found, almost lost, and found again

Hamilton thought that quaternions were his greatest idea and he applied them to a great many areas of mathematics and physics, but they fell into obscurity in the early twentieth century, becoming mostly a mathematical curiosity. The reason was that vector analysis was adequate to most purposes where quaternions had been applied. However, in recent years there has been a major renaissance in their use and study, because they are very useful in many areas of current interest that revolve around the rotation of three dimensional space or of objects in three dimensional space. Consequently, they are used extensively in astrophysics and astronautics, in computer graphics, and in quantum mechanics. For instance, Maxwell’s four equations, which may be written as four equations in vector analysis symbolism, are a single equation in quaternion notation. Dirac’s spinors, in quatum mechanics are a form of quaternion. There has also been a flurry of books and papers on quaternions. Three of the most recent are those by Kuipers (Kuipers 1999), Altmann (Altmann 1986 (reprinted in 2005)), and Hanson (Hanson 2006).

The algebra of quaternions

The algebra of quaternions is much like that of real and complex numbers. We can quickly summarize the basic rules of quaternion algebra.

Definition: A real quaternion is an ordered quadruple of real numbers, written , where a, b, c, and d are real numbers.

If and , then the fundamental definitions are as follows.

Equality:

Addition:

Multiplication by a scalar l:

Negative: .

Subtraction:

The zero quaternion:

These lead to the following rules that also apply to the algebra of real and complex numbers.

Note that quaternions of the form act exactly like real scalars, therefore the 1 is generally dropped. It is also straightforward to demonstrate that i, j, and k can be expressed as an orthogonal set of basis vectors. Consequently, a quaternion, may be expressed as the sum of a scalar, ‘a’, and a vector, . Thus, a quaternion may be expressed as -

On notation

Let us pause for a few remarks on notation. The expression that was just written illustrates the general format that is used here: . A symbol of the form or is an operator, in this case operating upon a quaternion. Quaternions are written in bold and italic (), vectors in bold (), and scalars in regular text (a). Of course, they are all technically quaternions, but it often helps to indicate which type of number we are considering. There tend to be fewer mistakes when one is forced to think about the nature of a variable. An operator uses square brackets and the letter is written in Helvetica font. The type of number is also indicated by whether the letter is in regular text, bold, or bold and italic. A norm () will always be a scalar, but a conjugate may be a vector () or a quaternion (). These conventions apply throughout this document.

There are more compact notations and they are occasionally used elsewhere, but this notation avoids ambiguities that sometimes arise with the more compact notations. Where the reader is expected to be more familiar with the manipulation of quaternions a denser notation may be appropriate. Here, we are striving for clarity.

Multiplication of quaternions

Quaternion multiplication is associative and distributive with respect to addition, but the commutative law, , holds only when one factor is a scalar, or the vector portions of both factors are proportional. Symbolically -

The scalar part of a quaternion product is not changed by the cyclical permutation of its factors.

Dissecting Quaternions: Tensor and Norm

Like complex numbers, there is a trigonometric form of quaternions. We start with the tensor and norm of the quaternion, essentially its length and its length squared, respectively. There are two norms of interest, the norm of the quaternion and the norm of its vector. Distance is defined essentially like in two-dimensional space.

The tensor and norm are both scalars. The magnitude of a vector or a quaternion may be written as and , respectively. The magnitude may also be considered the absolute value of the quaternion or of its vector.

Trigonometric Representation

Given the norms of the quaternion and its vector, we can write it as a magnitude times a unit quaternion.

This hardly seems like an improvement, but it can be simplified by noting that the sum of the squares of the scalar and vector terms is 1.0.

So, there is a , such that and . The vector component has a magnitude of one, so it is a unit vector. Consequently, we can write the expression in a much simpler, trigonometric, form.

The angle, q, is called the angle of the quaternion and the vector, v, is the unit vector of the quaternion. It happens that this form of the quaternion is often more useful for our purposes, because it directly relates to the action of the quaternion.

Conjugates of complex numbers and quaternions

There is one other definition that will be useful as we go along, so it will be described now. For complex numbers there is an entity called the conjugate of the complex number. It is essentially the reflection of the complex number across the real axis. The conjugate is the complex number with the negative of the imaginary part, . The conjugate has the nice feature that a complex number times its conjugate is its norm; . Quaternions also have conjugates and they are similarly defined. The conjugate of a quaternion is the quaternion with the opposite vector, but the same scalar –

.

The vector of the conjugate of a quaternion is the vector of the quaternion reflected through the origin.

It is true of quaternions as well that the product of a quaternion and its conjugate is its norm.

If the If Unit quaternions are frequently encountered, because they represent rotations in three-dimensional space.

There are a number of useful relationships that may be developed at this point. To start with we can restate the product of vectors in a slightly different form.

and changing the sign of the determinant is equivalent to interchanging the second and third rows, therefore -

More generally, the product of two quaternions is equal to the product of their conjugates taken in reverse order -

We can use this property to compute the norm of a product.

and, since is a scalar,

Stated formally, the norm of a product of two quaternions is the product of their norms.

Generalizing, by induction, it follows that -

It can be shown that the most general linear associative algebra over a field of reals, in which a product is zero only when one factor is zero, is the algebra of real quaternions. The quaternions include the real numbers (x, 0, 0, 0) and the complex numbers (x, y, 0, 0), both of which are fields, that is they closed under addition, subtraction, multiplication, and division. In addition, the quaternions include vectors in a space of three dimensions, (0, x, y, z). However, it was shown above that the product of two vectors is generally not a vector, but a quaternion, that is, a scalar plus a vector.

The multiplicative inverse of a quaternion

Quaternions form a division algebra, meaning that any quaternion can be divided by any other quaternion as long as the second quaternion is not zero. A particularly interesting quaternion is the inverse of a quaternion. We will now consider that object.

If and , then we may write the definition of the norm as follows -

Therefore we can define the reciprocal of q to be -

and thus

This shows that , or . In words, the magnitude of q is the reciprocal of the magnitude of the reciprocal of q, which is what one would expect.

In order to divide p by q (q≠0), we must solve the equation or the equation for the quaternion . This can be done by multiplying by , on the right in the first equation and on the left in the second. Thus and yield and , respectively. In general, . The quotient may be called the left-hand quotient and the right-hand quotient.

The norm of either quotient is equal to the quotient of their norms –

.

The reciprocal of the product of n quaternions is equal to the product of their reciprocals taken in reverse order -

From the definition of the reciprocal it follows that the reciprocal of a unit quaternion is its conjugate

and the reciprocal of a unit vector is its negative

In geometrical terms, the inverse of a quaternion has a vector that points in the opposite direction and the tensor of the inverse is the reciprocal of the tensor of the quaternion. The angular excursion is in the same direction.

Interpretation of quaternions as rotations

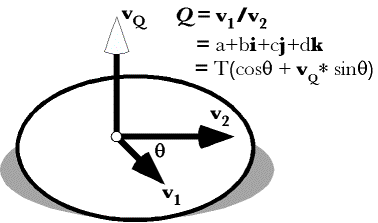
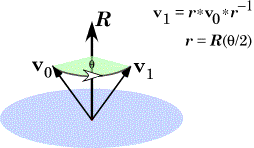
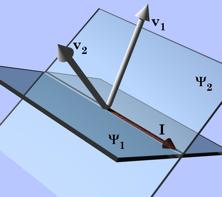
A quaternion may viewed as a rotation of one vector, , into another vector, . The axis of rotation is the vector of the quaternion (the golden vector), the angular excursion of the rotation is the angle of the quaternion, and the ratio of the lengths of the vectors is the tensor of the quaternion.

Quaternions, as we have considered them up to this point, are a pure mathematical abstraction. As such, they are very elegant, quite beautiful, but as an abstraction, they can be difficult to mentally assimilate. There is an interpretation of quaternions, one that starts with Hamilton, that makes them much more concrete and extraordinarily useful. Consider two different vectors in three-dimensional space. Bring them to together so that they have common origin. Choose one to be the starting vector, and the other to be the ending vector, . Assume that there is an operation that will transform the starting vector into the ending vector, what characteristics should it have? If is not the same length as , then there should be a number, , that is multiplied times to obtain . We might also notice that the two vectors define a plane and one can construct a perpendicular to that plane through the common origin of the two vectors, so that the starting vector rotates about the perpendicular until it is aligned with the ending vector. The vector perpendicular to the plane might be and the angular excursion might be the angle . It can be shown that if we write these parameters in the form of a quaternion, then the ratio of the two vectors is the quaternion.

Quaternions can be interpreted as ratios of vectors. In fact, that is effectively the definition of a quaternion.

This relationship turns out to be an immensely powerful and useful tool in analyzing movements in space. It allows one to often write down a description of a rotation by inspection. If one can imagine the axis of rotation by pointing one’s thumb in the direction that allows one’s fingers to curl from the direction of the starting vector in the direction of the ending vector then the direction of the thumb is v and the angular excursion is q. Normally one uses the right hand, but, as long as one consistently uses the same hand, all the calculations will be consistent and correct.

Conical rotations

A conical rotation is the rotation of a vector about an axis of rotation that is not perpendicular to the rotating vector. The new value of the vector is given by the expression , where the quaternion r is the rotation quaternion, R, written with half the angular excursion.

As long as we are describing rotations in a plane, the definition of a quaternion is totally adequate for the job. However, many rotations are not about an axis perpendicular to the rotating vector. The rotating vector may sweep out a conical surface. Such a rotation is a conical rotation. The argument for the formula that describes such a rotation is not straight-forward to derive, but the formula itself is not complex (Joly 1905; Kuipers 1999). If the rotating vector is and the axis of rotation is , the angular excursion , and the final length T times the starting length, then the final vector is given by the following expression.

In anatomy, the rotating vector generally does not change length, so the formula can often be written by inspection.

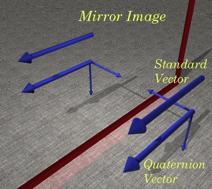
Since it can be difficult to be sure that the axis of rotation is perpendicular to the rotating vector and in most cases it clearly is not, it is generally best practice to use the formula for conical rotation to compute the consequences of a rotation.

When it is important to determine if two vectors are perpendicular, one can take their ratio. If the ratio is a vector, then the angle between the two vectors is 90°, because the scalar of the quaternion is equal to zero and .

Quaternion vectors are orientable

That last observation, that the ratio of orthogonal vectors is a vector, a quaternion with a scalar equal to zero, has interesting implications. A quaternion vector may be interpreted both as the directed magnitude and as the plane that is perpendicular to it. Beyond that, a vector is the ratio of any two mutually orthogonal vectors in that plane that stand in a particular relationship to each other. If we pick two vectors and and if is the ratio of to , then a rotation through radians about the vector must carry into . In effect, the quaternion vector is orientable. Vectors in vector analysis are not orientable.

In physics, some vectors, like forces and displacements, are not orientable, but others, like torque and spin, are. Reflection of a non-orientable vector in a mirror does not change it. Reflection of an orientable vector in a mirror reverses its polarity. The cross-product of the reflections of two vectors is not the same as their cross-product. It points in the opposite direction.

The standard vector of vector analysis is not orientable; it is indistinguishable from its mirror image. Quaternion vectors are implicitly the ratio of two vectors in the plane perpendicular to the vector, which lie in a particular relationship to each other. The mirror image of a quaternion vector is different in such a way that it is impossible to rotate or translate it in such a way as to superimpose reflection upon the reflected vector. Variables such as force and location may be standard vectors. Torque, angular momentum, and spin may be quaternion vectors.

Orientation and Frames

While quaternion vectors are orientable, they are not uniquely oriented. To settle on a particular orientation, it is necessary to choose a particular vector in the plane of the quaternion. If we choose a set of three mutually orthogonal unit vectors, then each vector is the ratio of the other two vectors and the array is uniquely oriented. An array of three mutually orthogonal unit vectors is a frame of reference, or just a frame. In a sense, a frame is a particular realization of a quaternion vector.

Frames are useful in the description of anatomical objects, because they are orientable, like anatomical objects. We can attach a frame of reference to an object by associating the various component vectors with features of the object. For instance, a frame may be attached to a hand by choosing one vector component to point in the direction of the middle finger, one pointing from the dorsum of the hand, and one in the direction of the thumb or little finger. Depending on the order in which we name the component vectors the frame may be right-handed or left-handed.

An important attribute of frames is that they do not have location. They transform differently than location when moved. There are vectors that do have location, such as the vectors that specify the position of an object in space. Such vectors assume an origin that is at a particular location and they extend to another particular location. Translation of either the origin or the location to which they point will change a location vector. Translation of a frame or of the space that it occupies does not change it. Rotation changes the values of frames. That is why they work well as indices of orientation.

Rescaling a space, that is allowing it to expand or contract uniformly, generally does not change orientation. However, some frames are used as indices of distortion in a medium. They have a definite orientation, but they are allowed to be stretched and/or compressed by expansion and contraction of the space they occupy and they are may be sheared by shearing distortions of their space. Their orientation is usually critical to the distortion that they experience.

The ratio of two planes in their intersection

Because a valid interpretation of a quaternion can be the plane to which the quaternion’s vector component is perpendicular, one is led to an elegant observation. If one has two planes, then their normals will codify the orientations of the planes. Since a normal to a plane does not have location, we can move it to take origin at a point where the planes meet. The angle between the planes will be the same as the angle between their normals. Consequently, the ratio of the normals will be the ratio of the planes. Since each normal is perpendicular to its plane and the ratio of the normal vectors must be perpendicular to each of the vectors, they define a plane orthogonal to both planes and the normal vector to that plane will lie in the intersection of the two planes. All of which leads us to the observation that the ratio of two planes is their intersection. The intersection is a quaternion that has its vector in the conjunction of the two planes and its angle is the angle between the planes. Since the normal vectors are usually unit vectors, the tensor of the intersection is a usually unity. It is a unit quaternion with a unit vector as its vector.

The ratio of two planes, and , is their intersection I. The quaternion, I, is the ratio of the vectors perpendicular to the planes, .

Example of the intersection of two surfaces

This observation about the intersection of planes can be applied to planes that are locally tangent to a curved surface. The tangent planes are defined by their normal vectors and if two surfaces intersect at a particular location, then the ratio of the tangent planes will define the direction of the line of intersection at the point of intersection. This can be illustrated by a simple example. Consider two unit spheres with their centers displaced distances ‘a’ and ‘b’ from the origin, along the ‘x’ axis.

The points of intersection are computed by determining when the two surfaces are equal.

If , then . Therefore, the points of intersection are readily computed.

For a sphere, the normal to the surface is always in the direction of a vector from the center of the sphere to the point on the sphere. Therefore, the two normal vectors at are as follows.

That leads us directly to the vector at the point of intersection.

If we plug some values for b into the expressions for the vector and the angle between the intersecting surfaces, then the reasonableness of the expressions can be checked by computing the ratio for a few sample values of ‘b’.

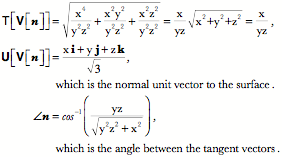
When a and b are equal to 1.0, then there is not a linear intersection, since the intersection is a point. However, the same tangent plane exists for both spheres, therefore the angle between them is 0°. For all the other intersections the line of intersection is vertical at the point where it crosses the horizontal plane at z=0. The coefficients of k are the sine of the angle between the tangent planes at the line of intersection.

The intersection of the tangent planes at points of intersection not in the horizontal plane through is given by the following expression.

It is a unit quaternion, therefore the angle of the quaternion is and the vector is the vector of the quaternion over .

Example of computing the normal to a surface

We can use the tangent plane to determine the normal to a surface. For instance, if we know two tangents to a surface, then the unit vector of their ratio will be the normal to the surface at that point. A simple example will illustrate this concept.

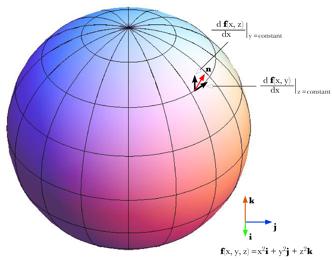
The tangent vectors can be computed by taking the partial derivatives with respect to an axis and then the normal vector is the unit vector of the ratio of the two tangent vectors.

Consider a unit sphere centered upon the origin.

The partial derivatives of y and z with respect to x are as follows.

Consequently, the tangent vectors are as follows.

The ratio of the two tangent vectors to the surface of the sphere at the point is –

The vector of the quaternion may be written as follows.

Then, the unit vector that is the normal vector to the surface of the sphere is then readily computed and it is precisely what is expected.

Ratios of Orientations

Frames express orientations and as an object moves in space it often changes its orientation, therefore, it is of interest to be able to mathematically express that change in orientation. Much as when considering the difference between vectors, the natural mathematical operation for comparing frames is a form of ratio. If we have two frames, then one way of expressing the spatial relationship between them is to write down the rotation that carries one into the other. For example, if the first frame is and the second frame is , clearly the rotation that rotates the first frame into the second is a 120° conical rotation about an axis of rotation aligned with the vector . The question is how do we obtain that result when the answer is not so obvious. A solution is to break the rotation into two component rotations. The first is to find the rotation that carries one axis of the first frame into the corresponding axis of the second frame. Then since both frames are sets of three mutually orthogonal unit vectors, the other axes for both frames must be in the same plane and the task is to find the angular excursion that rotates one of the other axes of the rotated first frame into the corresponding axis of the second frame. Let us consider the calculation that finds the ratio of the two frames given here.

It does not matter which axis is used, the calculation is essentially the same. In this instance let the first axis be the one used. A rotation that carries it from its direction in the first frame to its direction in the second frame is the quaternion that is the ratio of those two vectors.

As usual, the convention will be that if the rotation quaternion is written as , then the rotation quaternion with half the angle will be written as .

Having determined the rotation that rotates i into j, we must multiply the other axes of the first frame to obtain their new directions.

The frame is the intermediate frame. We pick another axis and take the ratio of the axes in the two frames to obtain a second rotation that brings the intermediate frame into alignment with the second frame.

We can multiply the intermediate frame by the rotation quaternion to obtain the second frame.

The rotation quaternion that rotates the first frame into the second frame is the product of the two rotations.

The result is precisely what we expected. That is a great deal of calculation to obtain the result that can be obtained by inspection, but it is generally not as easy to guess the correct axis of rotation and angular excursion. The approach laid out here will work equally well for all ratios of frames and it is easily written as a computer program that does the calculation and spits out the answer with a minimum of fuss.

The ratio of orientations is a remarkably useful concept in many situations. Even when the actual trajectory followed between two states is not a conical rotation. It is often useful to know what the equivalent conical rotation would be. In general, the equivalent conical rotation is the path that requires the least imposition of external control parameters. In the case of saccadic eye movements a model based on equivalent conical rotations gave the simplest explanation of eye movement control, one apparently consistent with actual experimental observations (see above).

Differentiation of quaternions

Differentiation of quaternions is much as one would expect (Joly 1905). The usual rules apply with the qualifications that arise from the imaginary components. If is a quaternion function of a single variable t, then the differential is the limit as approaches zero.

Consider an example.

It is noteworthy that the differential does not disappear from the expression as happens with functions of real numbers. That is because of quaternion multiplication being non-commutative. A similar thing happens with differentials of scalar functions of two independent variables.

Consequently, the retention of the differentials is not peculiar to quaternions.

The rotating vector

A simple example of the application of differentiation is the rotating vector. A fixed length vector, , is rotated in a plane that has the normal vector, .

The vector is perpendicular to the vectors and. Consequently, the trajectory is a circle in the plane perpendicular to , the plane of the rotation quaternion.

The first and second derivatives of the expression give the velocity and acceleration of the rotating vector.

If there is a mass at the end of the vector, then the force experienced as it rotates is directed inwards towards the center of rotation. That is the force required to maintain it upon its trajectory, that is, the force necessary to overcome its inertial tendency to continue in a straight line. The velocity of the mass is perpendicular to the rotating vector and the axis of rotation, in the plane of the vector’s rotation, pointing in the direction that completes a right-handed frame with the axis of rotation as the first component and the initial value of the rotating vector as the second component. The unit vector in the direction of the velocity is the ratio of the unit vector in the direction of the rotating vector to the unit vector in the direction of the axis of rotation.

The conically rotating vector

The expression is a bit more complex if the rotation is a conical rotation. The formula for a conical rotation gives the following expression.

If the rotating vector is perpendicular to the axis of rotation, then and , therefore the expression reduces to the expression give above except for having where occurs. That is what one expects, but it is reassuring to see that this complex expression reduces to the much simpler expression in the appropriate conditions.

This expression is difficult to interpret, but it does give an accurate description of a rotating vector that sweeps out a conical surface. The first and last terms are vectors and the two middle terms are related quaternions. All four vectors or vector products are constants that are modulated sinusoidally by their scalar coefficients. Consequently, the derivatives are functions of the scalars.

and

The vector products and are quaternions. Their vector components are equal and opposite in their directions, both perpendicular to the plane defined by and . Their scalar components are the same. Consequently, the difference between the two quaternions is a vector of twice the magnitude in the direction of the vector of .

The sum is always perpendicular to , in the plane it defines with . Consequently, it always points away from .

The upshot of these observations is that the velocity and acceleration are the sum of two perpendicular components producing a resultant vector in the plane perpendicular to , that is, the plane of the rotation quaternion. The end of the rotating vector moves in a circle and the velocity and acceleration vectors also move in circles shifted 90° and 180°, respectively, relative to the rotating vector.

When the rotating vector becomes perpendicular to the axis of rotation, the expressions for velocity and acceleration simplify to the resultants of two mutually perpendicular vectors in the plane of the rotation quaternion.

Since and are perpendicular, their product quaternion has a scalar equal to zero (cos 90°), therefore it is a vector. While these look different from the expression derived for the vector rotating in a plane, they are formally the same.

Derivatives of Orientation

Because the three components of a frame are mutually perpendicular, the rotation of a frame always involves conical rotation. Consequently, the derivatives that have just been considered are central to the description of continuous changes in orientation.

There are situations where the first or second derivative of orientation may be relevant. For instance, in a feedback system the rate of change of orientation may be a useful parameter of the change. If the rate and direction of a movement is a function of the difference between the current orientation and the final goal, then we can express the movement as a differential equation. It appears that natural movements are in some sense optimalized, especially if they are practiced or stereotypical. For instance, saccadic eye movements are constrained by the anatomy of the eyeball and the effort of maintaining the retinal image in a particular orientation. That is the implication of Donder’s Law and Listing’s plane (see above) (Tweed and Vilis 1987; Tweed and Vilis 1990; Tweed, Misslisch et al. 1994). All rotations that are not confined to a plane introduce a concurrent spin and there is not a mathematical necessity for the spin to be appropriate to the final location of the moving element. However, in the case of the eyeball, the orientation of the eyeball is appropriate for the direction of gaze, no matter what series of saccadic and smooth eye movements were used to attain it. This particularly apparent when the saccadic eye movements are between gazes that are at some distance from neutral gaze. A saccadic eye movement that followed the most direct path between the two gazes would end with an inappropriate amount of spin and it is not observed that the eye corrects the orientation at the end of the saccade. The correction occurs during the saccade, so that the eye arrives at the proper gaze with the appropriate orientation. Therefore, there must be some mechanism to ensure that the movement follows the trajectory that will automatically compensate for the necessary spin without introducing inappropriate spin. Such corrections will automatically occur if the eye follows the trajectory that is the ratio of the final gaze to the initial gaze (Langer 2005l). Such gaze shifts are not the shortest trajectories, but it turns out that they generally deviate from the geodesic connecting the two gazes by an almost inappreciable amount.

Experimental results indicate that something of this nature is in fact the way that saccadic eye movements are programmed. The main problem with this approach is that it is unlikely that the brain actually computes the ratio of two orientations in the manner that is done here. It turns out that there is a simpler, more natural, way to achieve this result. The combinations of gaze direction and gaze orientation allowed during fixation and smooth eye movements define a curvilinear surface of muscle lengths versus gaze direction (see the cover illustration of this book). In order for the saccadic eye movement to follow a trajectory that ends with an appropriate amount of spin, all it has to do is move in that surface. The input for the saccade generator simply has to be the final gaze direction of the desired saccade. The neural net that is used for smooth eye movements and fixation will guarantee that the eye lands on target with the correct orientation. The system is obviously more complex than that, because a large part of the saccade is the burst, which overcomes viscosity, compensates for the viscoelastic properties of the eye muscles, and accelerates the eyeball. The drive does not have to be as accurate as the tonic signal as long as it starts the eye in the right general direction, however it does seem to be reasonably accurate and well matched to the size and speed of the saccadic eye movements (Scudder, Kaneko et al. 2002). It is likely that the control lies in structures that are several links back into the system from the motor neurons, perhaps in regions that control both the saccadic bursts and the tonic drive.

Bibliography

Altmann, S. L. (1986 (reprinted in 2005)). Rotations, Quaternions, and Double Groups. Mineola, New York, Dover Publications, Inc.

Baez, J. C. (2002). "The octonions." Bull. Amer. Math. Soc. 39: 145-205.

Conway, J. H. and D. A. Smith (2003). On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd.

Hanson, A. J. (2006). Visualizing Quaternions. Amsterdam, Elsevier.

Joly, C. J. (1905). A Manual of Quaternions. London, Macmillan and Co. Ltd.

Kuipers, J. B. (1999). Quaternions and Rotation Sequences: A Primer with Applications. Princeton, New Jersey, Princeton University Press.

Langer, T. P. (2005e). Structural Ratios: The Comparison of Structures and Their Parts.: http://homepage.mac.com/tlanger_sasktel_net/Theory/quaternions.html.

Langer, T. P. (2005l). The Static Gaze Surface and Null Spin Saccades: Spin Neutrality and Saccadic Trajectories.: http://homepage.mac.com/tlanger_sasktel_net/EyeMovements/eyemovements.html.

Scudder, C. A., C. S. Kaneko, et al. (2002). "The brainstem burst generator for saccadic eye movements: a modern synthesis." Exp Brain Res 142(4): 439-62.

Stewart, I. (2007). Why Beauty is Truth. A History of Symmetry. New York, Basic Books.

Tweed, D., H. Misslisch, et al. (1994). "Testing models of the oculomotor velocity-to-position transformation." J Neurophysiol 72(3): 1425-9.

Tweed, D. and T. Vilis (1987). "Implications of rotational kinematics for the oculomotor system in three dimensions." J Neurophysiol 58(4): 832-49.

Tweed, D. and T. Vilis (1990). "Geometric relations of eye position and velocity vectors during saccades." Vision Res 30(1): 111-27.