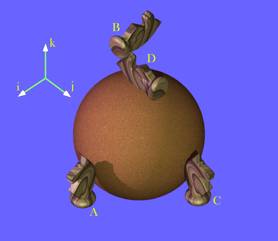
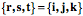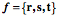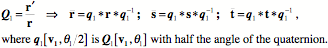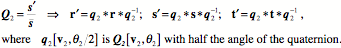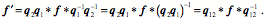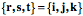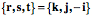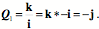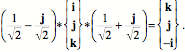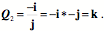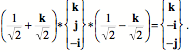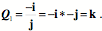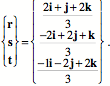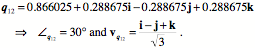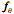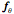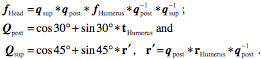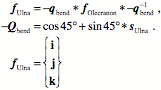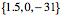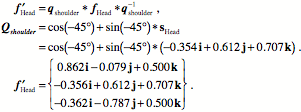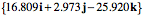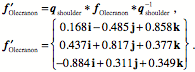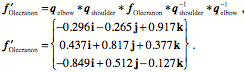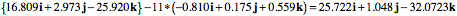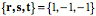Transformations of Orientation: Revisiting Swing and SpinLet us return to the concepts of swing and spin and try to put them on a more precise, quantifiable, basis (Standring 2005). Consider their properties. In a spin the object does not change its location, but it does change its orientation. In pure swing the object changes its location, but its entire trajectory lies in a single plane. If the arc is about a center that does not lie in the plane of the movement, then it is called swing. The movement in a general swing is a conical rotation. The key to swing is the change in both orientation and location. Change in location without changing the orientation of the object is a translation. Transformations of orientation are not intrinsically either spin or swing, because orientation does not have location, but the change in orientation that occurs during the movements is central to understanding those concepts (Langer 2005b; A simple example
The knight stands in here as a simple orientable object. The different images of the knight are placed adjacent to a sphere to illustrate the movements of the knight as excursions on the surface of the sphere. Orientation does not have location, consequently, the different versions of the knight may be placed in any order in space. However, this ordering illustrates the relationships between movements and orientation. Knight B is obtained by rotating knight A 90¡ along the vertical meridian. Knight D is obtained by moving knight A 90¡ to the right to C and then 90¡ along the vertical meridian to D. Clearly orientations, B and D, are different, although all the trajectories follow great circles, therefore introduce no spin. Null SpinDuring a pure swing, orientation changes in a special way. The orientations assumed by an orientable object as it travels along a great circle arc are said to have null spin relative to each other. There is null spin because movement along a great circle is pure swing, meaning there is no spin. That means that although the orientation changes the axes maintain their sense. In the above illustration the knight at C is oriented so that it looks away from the center of the sphere with its head directed towards the north pole and its left side directed to the east. The same sort of relationship exists between A and B and C and D, but not between B and D. If B and D are superimposed, so that they had the same location, then it would require a spin to convert one into the other. Note that location is key. If D were translated to a position opposite C and B were translated to a position opposite A, then they would have null spin relative to each other, but they would have 180¡ of spin relative to the knights situated opposite them. In general, if a knight travels along different great circles to the same location, which would have to be an antipode, then the orientations of the two images of the knight will be rotated relative to each other. If the orientation frame of reference is centered upon a point in the surface of a unit sphere, then the excursion it experiences in pure swing is comparable to its following a great circle on that unit sphere. We might use the familiar example of the geographical globe to illustrate this point. For instance, if the origin of the frame lies upon the equator with its first vector, r, pointing perpendicular to the surface of the sphere, its second vector, s
However, r continues to point directly away from the center of the sphere, s The term null spin has the potential to be confusing, because an orientable object does rotate as it moves along a great circle on the surface of a sphere, but all of the rotation is accounted for by its change in location, therefore it has no spin in the technical sense used in kinesiology. Consider what occurs if the frame moves along the equator through 90¡. The values of the frames vectors change in a different manner, but all orientations obtained by traveling along the equator have null spin relative to each other. One may appreciate that by noting that the r Consequently, there is a type of equivalence that exists between the orientations that a frame experiences as it moves along a great circle. All the orientations along the vertical meridian have null spin relative to the initial orientation and all the orientations along the equator have null spin relative the original orientation. Note, however, that, with the exceptions of the initial orientation, orientations along the vertical meridian excursion do not have null spin relative to orientations along the equatorial excursion. That is easily demonstrated by considering the consequences of moving 90¡ along the equator and then 90¡ along the vertical meridian from that point, to bring the frame to the north pole.
Each of the swings is a great circle, therefore all the orientations experienced by the moving frame have null spin relative to the their starting orientation, but the final orientation has a clear spin relative to the orientation obtained by moving directly north on the vertical meridian.
For orientation, null spin equivalence does not transfer. If we use the symbol, Ratios of OrientationsThe property of having null spin relative to a standard orientation will be called spin neutrality. Spin neutrality may seem like a rather arcane concept, but it lies at the foundations of an understanding of spin and swing. To address this point it is necessary to introduce a second concept, the ratio of orientations. To start, note that all possible orientations may be expressed as a frame of reference and that any orientation may be transformed into any other orientation by a rotation about a single axis of rotation. In general, the axis of rotation is not parallel to any of the axes of the frame of reference and no axis in the final frame is parallel with its direction in the initial frame. The problem that needs to be addressed is how one can determine the axis of rotation and the angular excursion that will carry the initial orientation into the final orientation. That information is expressible as a quaternion. So we are searching for a method that will yield the quaternion that is the ratio of the final orientation to the initial orientation. One method of finding the ratio of two orientations uses the definition of a quaternion. Assume that you have a frame of reference for an object prior to a rotation
Once we know the rotation quaternion, it is possible to compute an intermediate frame,
The vector of the quaternion will be the The quaternion that expresses the rotation that carries f
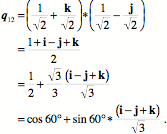
The transform associated with An Illustrative ExampleLet us apply this tool to the example that we considered above, that is, the rotations to the north pole by two different routes. The starting orientation (A) is
When we multiply the initial orientation by the quaternion the results are the final orientation.
The final orientation of the second trajectory has the same first quaternion, because the r axis is the same in that orientation as it is in the first transformation. Therefore, we can address the second quaternion ratio of the orientations. Let the chosen axis be the s axis.
One can see by inspection that it is the correct axis of rotation, but multiplying out the expression confirms that the quaternion rotates the intermediate frame of reference, in this case B, into the final frame, D.
Consequently, we can write down the quaternion that rotates the initial orientation into the final orientation for the two-step trajectory.
This means that if we rotate the initial orientation 120¡ about an axis that passes through the front left upper quadrant Alternative InterpretationsNote that in the first calculation, for the great circle trajectory, it is also possible to have chosen the s In addition, it seems that, in common practice, the term spin is often taken to imply that the rotation is about an axis of the frame of reference. However, since the axes of a frame of reference are seldom explicitly defined, it is difficult to be sure of this requirement. Let us reexamine the two-stage trajectory, this time choosing the ratio of the s axes as the first quaternion. The first quaternion is readily computed.
If you multiply the initial frame of reference by the half angle version of the first quaternion, then the intermediate frame is
The first rotation is a 90¡ rotation about the t If you choose the t axis for the first quaternion then the ratio is i Consider another ratio of frames, related to the one just considered, but a bit less obvious. The original frame of reference is the same,
The first quaternion for the ratio, based on aligning the r
The second quaternion is a 36.8699¡ rotation about the r
When we compute the half angle forms of these rotation quaternions and multiply them together, the result is - The intermediate steps do not give obvious values, such as one might write down from inspection, but the end result is that the final orientation is equivalent to rotating the initial frame of reference 60¡ about the unit vector that lies at the center of the forward upper left quadrant of the universal coordinate system. The power of quaternion analysis becomes apparent when one becomes involved with problems in which the angles and axes of rotation are not convenient multiples of pi, especially when using a computer that has a programmed function to take the ratios of frames, which would be the normal way of obtaining this result. Uses for the Ratio of FramesThe ratio of frames is a very useful tool when describing the anatomy of a jointed orientable object, such as a humerus. If the location of the bone is known, along with its orientation, then one can express the location of other features as extension vectors written in terms of the frame of reference for the bone. The orientations of the facet joints can be written as rotations of the boneÕs frame of reference, that is, a quaternion. Using the ratio of the frames is much more efficient than listing all the associated frames of reference explicitly. The vector of the ratio quaternion transforms like an orientation vector, so rotations of the bone can be applied directly to the ratio of the frames and the new frame can be obtained by multiplying the frame of reference by the ratio quaternion. Such relationships, where two orientations remain in a fixed relationship to each other, will be called linkages Another type of relationship can be defined for the bones on the two sides of a joint. A frame of reference can be defined for the bone on each side of the joint, when the joint is in a particular configuration. Such a relationship can be expressed as a ratio of the two frames. However, the spatial relationship between the two frames may be changed by rotation about an axis of rotation, which is a description of the joint action. We can define the jointÕs action as the ratio between two orientations of the moving bone. For instance, if These concepts can be better appreciated by using them in an a example. We will now consider a problem that involves the bones of the arm and forearm. Both types of frame ratio will be used. An Illustrative ExampleLet the humerus suspended at rest from the glenohumeral joint be in its neutral position. The frame of reference for the bone will have the r axis directed straightforward, the s axis directed medially, and the t axis directed superiorly. Let the universal coordinates be such that the frame is aligned with them.
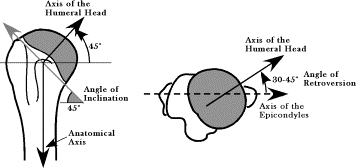
Then the head of the humerus is rotated about 30¡ posterior to the frontal plane and tilted 135¡ up relative to the shaft of the humerus.
If we evaluate these expressions, the frame of reference for the head has the s axis directed to the center of the articular surface, the r axis is directed anteriorly and medially, and the t
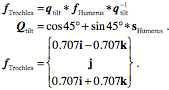
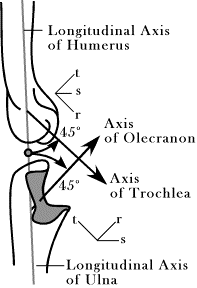
The trochlea of the elbow joint is tilted about 45¡ superior relative the long axis of the humerus, but, for present purposes aligned with the long axis of the bone, with its axis of rotation directed medially. Because the articular surface is a spiral, the axis of rotation will shift as the angle between the humerus and the ulna change, but that complication will not be introduced here. The frame of reference will be given by the following expression, where the r axis points anterior and inferior and the t axis is directed anterior and superior. The s
The sense of the olecranon process of the ulna is rotated about 90¡ superiorly, about a medially directed axis. Consequently, the frame of reference for the olecranon process is expressed relative to the frame for the trochlear as follows.
At rest the frame of the ulna has its r
If we know the orientation of the olecranon, then the orientation of the ulna can be computed by inverting the relationship.
The center of the humerus ( Now, consider the effect of a 45¡ rotation in the shoulder about the s axis of the humeral head and a 30¡ rotation about the axis of the trochlear/olecranon joint so as to flex the ulna on the humerus. First, it is useful to write the descriptions of the two bones from the perspective of the head of the humerus. The humeral head is set to The orientation of the head of the humerus will be rotated by the shoulder movement.
The orientation of the humerus is obtained by applying the rotation at the shoulder to the initial orientation.
The center of the humerus swings to
The orientation of the olecranon process after flexing the shoulder and prior to flexing the elbow may be computed in the same manner.
After both operations the new orientation is the product of the two quaternions. We obtain the axis of rotation at the elbow from the s
The orientation of the ulna is straightforward to compute, since its description prior to the movements is simple.
The location of the middle of the ulna is the location of the olecranon plus eleven times the negative t axis for the frame of the ulna.
The distal end of the ulna lies at Using the methods developed to this point, it is possible to compute the locations, extensions, and orientations of any bones moving about any joint with an accuracy commensurate with the accuracy of their anatomical descriptions. However, it is often easier to appreciate these results if they are used to generate images that illustrate the movements of the bones. The next section considers such a calculation. Arm Swing
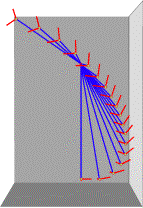
The blue lines represent a humerus that is swinging about an axis of rotation that is tilted into the center of the anterior lower left quadrant The methods used in the last section can be used repeatedly to plot the excursion of a movement. In the above figure, the placement of the humerus has been computed for a series of 10¡ rotations about a fixed axis of rotation. In the illustrated example, the axis of rotation is approximately the central axis of the humeral head. It is tilted 45¡ anteriorly, 45¡ caudally, and 45¡ laterally. In a sense, this is pure flexion in that the rotation is a spin about the central axis of the humeral head. The curved trajectory is due to the facet surface being tilted superiorly and medially.
Langer, T. P. (2005b). Modeling Rotations of Orientable Objects in Three Dimensions: An Introduction to Quaternions and Framed Vectors.: Langer, T. P. (2005c). Geometrical Anatomy and Anatomical Movements: An Introduction to the Use of Quaternions and Framed Vectors in the Description of Anatomical Rotations. : Langer, T. P. (2005d). Commentary on JolyÕs Manual of Quaternions Langer, T. P. (2005e). Structural Ratios: The Comparison of Structures and Their Parts.: Langer, T. P. (2005f). The Geometrical Anatomy of Compound Movements.: Standring, S. (2005). Gray's Anatomy. The Anatomical Basis of Clinical Practice. Edinburgh, Elsevier Churchill Livingstone.
|
. 
transform is a rotation about the frame axis that was chosen for the first ratio. The actual first and second quaternions will depend upon the axis chosen for the first transform. However, the combined transform will be the same no matter which axis is chosen for the first transform.
, then it will have the final orientation indicated by the knight labeled D in the above illustration.
. Since the final orientation is 
, it is straightforward to compute the second quaternion, by choosing one of the other axes, and then the equivalent rotation.
. Consequently, the equivalent rotation is the same as in both the other calculations. In this instance, the first rotation is a 90¡ spin about the r
is the axis of rotation for the joint moving between those placements. Unlike the other ratios of frames, such a joint rotation quaternion has a location, which may be written as one of the extensions of the bone. Variable ratios of frames, such as exist in joints will be called concatenations
) at about 
