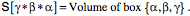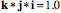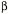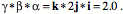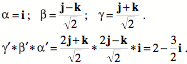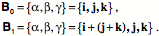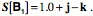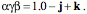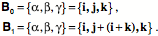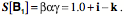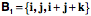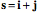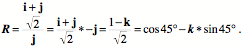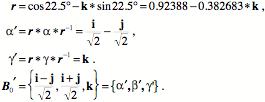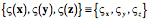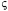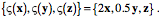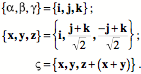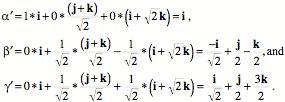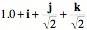Distorting the box: Strain in Anatomical Media Up to this point we have been concerned with situations in which the object under study remains rigid. Consequently, the frame of reference has remained rigid and rotated as a unit, without changing the relationships between the axes of the frame. Now we will consider what happens when we allow the frame of reference to be distorted by shear, compression or stretching, as well as experiencing translations and rotations. In a word we will consider strain (Langer 2005v;
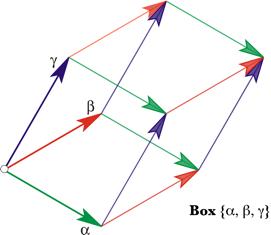
The box at a point in the matrix is defined by three edge vectors, The Triple Vector ProductTo start, consider an interesting feature of quaternions. Assume that we have a box defined by three vectors, each in a differently oriented edge of the box. While it is not necessary, it is convenient to choose three edges that take origin from the same corner. Let the edge vectors be designated by the symbols a,
If the three edge vectors are
Any three mutually orthogonal vectors will have a product that is a scalar, therefore the volume of the box that they define will be the product of the three vectors. That follows from the observation that the product of any two orthogonal vectors is a vector that is perpendicular to the plane that they define. Therefore, their product is parallel with the third vector and it can be expressed as a scalar multiple of that vector. The square of any vector is a scalar equal to its length squared. Consequently the triple product of three mutually perpendicular vectors is a scalar. Test BoxesA frame of reference is composed of three mutually perpendicular unit vectors, therefore the volume of the box defined by a frame of reference is unity. It follows that if we sample a distensible medium by placing a frame of reference at some point within it, then we will start with a unit cube of material. As the material is locally deformed, the box will be deformed. In fact, we can define the local strain at a point by dispensing with the other edges and retaining the three corner vectors that start at that point. Since frames of reference do not have location, it will be convenient to give this sample a different name, so, let us call it the unit box at that point. However, there is no implication of a particular volume of material. A unit box may be infinitesimal, if need be. It is the relationships between the edge vectors that will be of interest, not the full box. In fact the formal meaning of a box will be an ordered set of three co-original vectors, the edge vectors Distortions of Test BoxesAs stretching or compression deforms the matrix of the material, the edge vectors will become longer or shorter. Those changes will be reflected, in part, in the volume of the box, which is equal to the product of the three edge vectors. The change in volume is the volumetric strain Consider a matrix that is stretched to twice its original length in the direction of the
Typically, the volume of a box does not change greatly when a biological material is strained, but the lengths of the edge vectors may change substantially. As a biological material is stretched in one direction, it contracts in the perpendicular plane. If it is stretched in a plane, it becomes thinner in the direction perpendicular to the plane. If the axes of a test box are aligned with the directions of the strain, either tensile or compressive, then they remain mutually perpendicular and the product of the three edge vectors remains a scalar, which is the volume. If the strains are not aligned with the edge vectors of the test box, then the vectors will not remain perpendicular. The product of the edge vectors will be a full-blown quaternion, with both a scalar part and a vector part. The scalar part of the strain quaternion remains the same, irrespective of the orientation of the test box. The vector component depends upon the orientation of the box used to assess it. This characteristic of the strain quaternion will be considered in some depth, below. A box set so that its edge vectors are in the directions that are expanding or contracting will not experience a change in the angles between the edge vectors. That is not generally true for all test boxes. However, pure compressive/tensile strain will cause an apparent shearing if the edge vectors are not aligned with the directions of change. The vectors may appear to converge towards each other (angles between the edge vectors less than 90°) or they may appear to diverge (angles between the edge vectors greater than 90°), or some may converge and others may diverge. Consider the same situation as in the last calculation, except that the
Note that the
The strain quaternion has a volumetric strain of 2.0 and a vector strain of 1.5 i. The angle of the strain quaternion is 36.87°, meaning that the Types of StrainThere are two types of strain that may occur separately or together. The first is the tensile or compressive strain, which was just discussed. The second is shear strain, which is produced when one face of a block of material is moved relative to the opposite face in a parallel plane. The first illustration in this section, of a box, was an example of shear strain. In compressive or tensile strain it is always possible to find a test box that experiences only volume strain. In a material that is experiencing a shear strain there is no box that experiences only volume strain. There is always a vector component to the strain quaternion, no matter how the test box is oriented. On the other hand, a pure shear strain, that is, one face of the box moving parallel to the opposite face, will not change the volume of the box, so the scalar of the strain quaternion remains the same. For a unit test box, the scalar is 1.0. In a tensile/compressive strain, the material is stretched in one or more directions or compressed in one or more directions. It is possible to have expansion or contraction in three orthogonal directions. A block of material placed in a vacuum, or one that is growing in a manner distributed through the material may expand in all directions. Similarly, if a block of material is compressed in a chamber it will experience shortening in all directions. If a block of material is stretched or compressed by moving attachment points around its periphery, then it may expand or contract in a plane or sheet that is distributed in two dimensions. If the block is stretched or contracted by forces applied to opposing faces, then it expands or contracts in one direction. In order to maintain a nearly constant volume in the material, the test box will experience the opposite type of change in the directions that are not constrained. Because of their high water content, biological tissues tend to be nearly isovolumetric in response to physical forces, when possible. In shear strain there is always a movement of the edge vectors of the test box so that the angle between two or more of the axes is no longer a right angle. There is no way that the test box can be placed such that the angles between the edge vectors all remain right angles. It is possible to choose a test box so that one of the edge vectors is in the direction of the shear and one is perpendicular to it. The third vector is tilted relative to the plane formed by those two vectors. That is the shear. It is clear that the relationships between the edge vectors of a strained box are an important index of the nature of the strain. That information is embedded in the vector component of the strain quaternion. We now turn to an examination of the relations between the edge vectors and the vector component of their strain quaternion. The Vector Component of a Strain QuaternionLet us start with a simple distortion of a box. The box is distorted by pushing the top face in the direction of the bisector of the other two axes. The descriptions of the test box,
The strain quaternion for the test box is 1.0, as it should be, since it is unstrained. The strain quaternion for the strained box is Consider another example. The a axis is sheared in the direction of the bisector for the second and third edge vectors.
If we compute the triple vector product as we did in the last example, then the strain quaternion is incorrect.
The vector of the strain quaternion is the negative of the vector that turns the a axis from the unstrained test box into the a axis for the sheared test box. A little experimentation will reveal that the triple vector product that yields the correct result is
If we choose the situation where the shear is in the direction of the bisector of the first and third axes, then the correct triple product is the one that starts with the b edge vector.
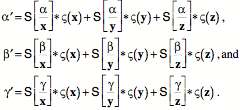
The general rule is that when an axis is sheared relative to the other two, then the strain quaternion is the triple vector product that starts with the sheared axis. The second and third elements of the triple product establish the perpendicular to the reference plane and the product of the sheared edge vector times the reference vector gives the axis of rotation of the sheared vector relative to the reference vector. Choosing the Test Box for Shear StrainNot all shears are going to occur parallel with a plane determined by two edge vectors of a randomly chosen test box. On the other hand, if the strain is a shear, then there will be a test box that experiences relative displacement of only one axis. Let us now consider how one might find such a test box. To explore the possibilities, let us return to the original example. The original test box was
We can now rotate the original test box to obtain a test box in which the second edge vector is aligned with the direction of the shear and the first and third edge vectors are perpendicular to it.
The scalar of the strain quaternion for this box is still 1.0 and, if the k is replaced by the sheared axis, the strain quaternion is It might seem that this approach might work in general, but it turns out that one cannot generally go directly from the distortion of an arbitrary sample test box that is produced by a strain to finding the test box that is aligned with the strain axes. In fact, the distortion produced by a strain may be quite dramatic if the test box in not aligned with the strain axes. We now consider two rather simple examples that illustrate the manner in which test boxes may be distorted by strains that are not aligned with the box’s edge vectors. Calculating Distortions in Test Boxes Not Aligned with the StrainLet us assume that we have an array of sample points in a biological matrix that experiences a strain and we wish to know how the strain will change the edge vectors at the sample points. That is relatively easy to determine if the strain is aligned with the edge vectors of the test boxes, because the strain affects the different vectors independently. For instance, the first edge shrinks by 10%, the second expands by 10%, and the third is unchanged, as might occur with a compressive/tensile strain, or the first two vectors are unchanged, but the third vector is tilted 10° in the direction of the second edge vector, as might occur with a shear strain. The situation is more complex if the compression occurs at an angle to all of the edge vectors or the shear is in a direction that is not aligned with any edge vector. Under such circumstances, there is an interaction with multiple axes and it is usually found that the edge vectors of the test box are no longer orthogonal. The test box typically looks squashed. To simplify the discussion of this type of situation, let us pause to define a new construct. A strain transform The relations between the edge vectors of the test box and the components of the strain frame will be the basis for calculating the strain that the test box experiences. Let the strain transform be expressed by the set of vectors
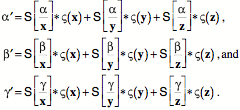
Now suppose that the test box,
The scalars are essentially the dot products of the two axes. Consequently, the scalar terms are the projections of the Similar expressions apply to the transformation of the
A Contraction/Expansion Example:
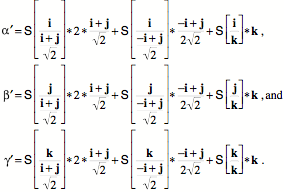
Let the strain transform be the one given above for expansion along the x axis and compression along the y axis. Then we can write down the new values of the edge vectors for the test box.
Which evaluates as follows.
If we expand the products and collect terms the result is as follows.
Consequently, the test box after the strain is Despite the transform being a simple expansion/contraction, the placement of the test box is critical to seeing the simplicity of the strain. A Shear Strain Example: For comparison, a similar example with shear will be considered. Once again, the parameters have been chosen to allow the calculations to be done manually. Let us keep the same test box, but let the shear be given by the following transform.
The strain is the same as was used above, except for being rotated 45° about the i axis in a positive direction. The calculation is much as it was for the previous example.
We replace the terms with their particular values.
Now, multiply the terms and collect common factors.
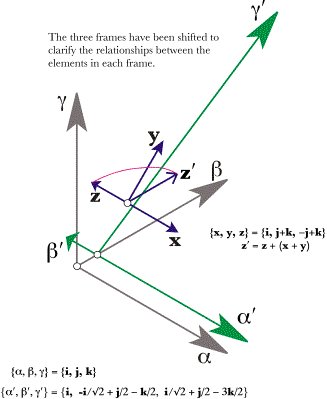
The strained test box is truly distorted by the shear strain, but it still has a volume of 1.0. The
The test box (gray) and the stained box (green) for the shear strain indicated in the stain transform (blue) have been drawn offset to clarify the differences between the frames. The The consequences of straining test boxes that are not aligned with the axes of strain indicate that it may be difficult to determine if a strained test box was submitted to a compressive/expansive strain or a shear strain, or a combination of both. As stated at the outset of this section, there are frames of reference for which the different strains are particularly simple. For instance, if a box is aligned with the strain axes for a shear strain, then the strain may be expressed as a tilting of one of the strain axes. Naturally, a question arises of whether one can work backward from a strained box to the alignment that is optimal for expressing the strain. The short answer is no, but it is interesting to see why not. The next section explores these issues by examining the manner in which unit spheres are distorted by strain. In some ways the use of spheres simplifies the analysis.
|