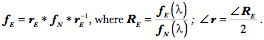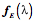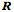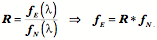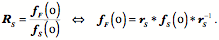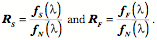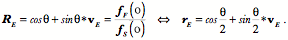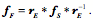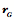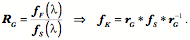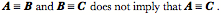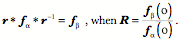Transformations of Orientation in a Universal Joint

The glenohumeral joint is a universal joint in that it has an infinite number of possible axes of rotation; it has potentially three degrees of freedom for location and three degrees of freedom for orientation. In practice, its location has two degrees of freedom because its position may be expressed by specifying 1.) the elevation or altitude and 2.) the azimuth of the central axis of the humeral head. These are comparable to latitude and longitude on a globe. The third degree of freedom would be the radial displacement, but that is nearly constant, because the articular surface of the humeral head is nearly spherical. Orientation of the humerus has three degrees of freedom because it can be expressed a standard orientation multiplied by a unit quaternion. A quaternion has four components, but a rotation quaternion is a unit quaternion and in a unit quaternion the vector is a unit vector, therefore if you know two of its components, you can compute the third.

Understanding the movements of the glenohumeral joint in these terms is certainly possible, but, it is complicated, because it is part of an assembly of bones and joints that are controlled by many muscles, some of which cross more than one joint. To simplify the problem of a universal joint, we can choose a model system in which the anatomy is simpler. The eyeball is such a model system. It is a nearly spherical object that rotates about a single center of rotation and it is controlled by six muscles with definite origins and insertions that remain relatively constant with respect to the orbit and the eye. There is also a clear functional constraint upon the placement of the eye, namely to keep the visual image consistently oriented upon the neural retina. These constraints greatly simplify the anatomy of the system while leaving most of the interesting features of a universal joint. Let us consider the anatomy of the eyeball and the implications for its movements. Most of the points raised here have been treated in more detail elsewhere (Langer 2005j; Langer 2005k; Langer 2005l).

The anatomy of the eye

The details of the relevant anatomy, which are considered below, are drawn from many sources (Cogan 1956; Cogan 1966; Cogan 1980; Leigh and Zee 1991; Demer, Miller et al. 1995; Williams, Bannister et al. 1995; Demer, Miller et al. 1996; Clark, Miller et al. 1997; Demer, Poukens et al. 1997; Clark, Miller et al. 1998; Clark, Miller et al. 1998; Clark, Isenberg et al. 1999; Clark, Rosenbaum et al. 1999; Clark, Miller et al. 2000; Demer, Oh et al. 2000; Thurtell, Kunin et al. 2000). Many of these sources describe the fibromuscular pulleys in the suspensory membrane, which have been examined in substantial detail using quaternion analysis (Langer 2005j; Langer 2005k).

The eyeball is nearly spherical, usually being somewhat longer in the visual axis than in the perpendicular directions (Standring 2005). It will be convenient to assume it is spherical for present purposes. That approximation will not make a significant difference for what follows.

The eyeball rests in a cushion of fat within a cone of muscles formed by the rectus muscles and their fascia, so that it rotates about a central point, which will be assumed to be on the visual axis where it intersects the mid-coronal plane of the eye, that is at the center of the sphere of the eyeball.

The eyeball is also suspended in a fascial membrane that coronally transects the orbit, like a basketball embedded in a drumhead (Demer, Miller et al. 1995; Clark, Miller et al. 2000). The suspensory membrane intersects the eyeball approximately at its equator. This feature of the eyeball is not generally a part of introductory descriptions of the eye and its orbit, but it has definite implications for the movements of the eye in the orbit (Langer 2005j; Langer 2005k).

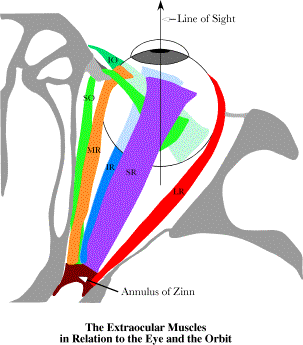
Six extrinsic eye muscles take origin from the walls of the orbit and attach to the eyeball in consistent locations. The line of sight in neutral gaze is at an angle to the gross pulling directions of the individual eye muscles. That may be functionally irrelevant, because the myofascial slings in the suspensory membrane effectively move the origins of the rectus muscles to the suspensory membrane.

Four extrinsic eye muscles extend from the annulus of Zinn, a fascial ring that encircles the optic nerve as it enters the orbit, to the anterior surface of the eyeball, surrounding the cornea at some distance. These four recti form a cone that surrounds the eyeball and its retro-orbital fat. They attach to the eyeball in four quadrants. The lateral rectus attaches lateral to the cornea, the medial rectus, medially, and the superior and inferior recti, above and below, respectively. The annulus of Zinn lies about 22° medial to the visual axis of the eye, so the lateral rectus needs to be longer than the medial rectus and the superior and inferior recti appear to pull medially as well as up and down. In fact, there are indications that the suspensory membrane that supports the eye is thickened around the muscles as they penetrate it, causing there to be fascial slings that hold the muscles in a relatively constant position as they pass through the suspensory membrane to reach their insertions. That anatomy turns out to be relevant to the dynamics of the eyeball (Langer 2005k).

There are two more extrinsic eye muscles that are different in that they reach from positions anterior to the equator of the eyeball back to attachment sites on the posterior lateral aspect of the eyeball. The inferior oblique muscle takes origin from the inferior margin of the orbital rim and attaches to the inferior lateral aspect of the eyeball, behind its equator. The superior oblique muscle takes origin from the annulus of Zinn, but has a long tendon that extends through a fascial sling on the superior medial rim of the orbit, the so-called trochlea, and then extends through the suspensory membrane to attach to the superior lateral aspect of the eyeball. The details of this orbital anatomy and the precise locations of the origins and insertions of the extrinsic eye muscle are given elsewhere (Langer 2005j). The mathematical description of the anatomy of the eyeball and the orbit turns out to be complex, therefore will not be written out here. A full description is given elsewhere (Langer 2005j; Langer 2005k). In this venue, we will explore the implications of the anatomy for eye movements.

Donder’s and Listing’s Laws

The eyeball is orientable. The natural choice of a frame of reference is to take the line of sight as the first axis and the horizontal and vertical meridians as the second and third axes. That will be the convention in what follows.

The eyeball is an orientable object and its orientation is based upon the line of sight and the vertical and horizontal meridians. When viewing the world, the optimal orientation of the eye is generally the one that maintains the vertical axis of the visual image upon the retina aligned with the vertical meridian of the visual field.

In the visual paradigm, the combination of line of sight and orientation that was called placement when considering joints is more logically called gaze. Gaze has a direction and an orientation. Since the line of sight is always parallel to the first axis of the frame of reference, it is convenient to compute gaze using just the frame of reference, but it is important to remember that the line of sight, or gaze direction, is different from the frame of reference, or gaze orientation.

First note that the combined actions of all the extrinsic eye muscles has the ability to move the line of sight to any direction within a wide solid angle about the line of sight in neutral position. With effort one can move an eye about 40° in any direction. In any of those directions, the eye is physically able to assume a range of orientations, that is rotations about the visual axis. In that respect the eyeball is a universal joint much like the glenohumeral joint. However, observation of actual eye movements indicates that, although a range of orientations is physically possible, the eye tends to assume a particular orientation for each direction of gaze. That preferred orientation is, logically enough, the one that keeps the visual image upon the retina as nearly like the image in neutral position as possible. This may be expressed by saying that the vertical axis of the visual image tends to remain parallel with the vertical meridian of the eye. Equivalently, the preferred orientation is the orientation that one obtains by moving along a great circle trajectory from neutral gaze position and orientation to the gaze direction.

Great circles are interesting, because they are the shortest trajectories connecting two points on a sphere. They are the geodesics of a sphere. It is convenient that the shortest paths between neutral gaze and an eccentric gaze will automatically attain the most desirable orientation of the eyeball. However, it turns out not to be the general rule. Much of what follows is addressed to explaining why geodesic trajectories are not generally satisfactory for eye movements, determining what trajectories are optimal, and exploring the properties of those optimal trajectories.

Donder’s law

Gaze at eccentric eye positions is predicted by multiplying neutral gaze by the great circle quaternion with a plane that contains both the line of sight for neutral gaze and the line of sight for the eccentric gaze. This relationship has been canonized as Donder’s law (Tweed and Vilis 1987; Tweed and Vilis 1990; Tweed, Misslisch et al. 1994).

If neutral gaze is and the direction of an eccentric gaze is , then the great circle trajectory from neutral gaze to the eccentric gaze is given by the following expression.

As usual, the quaternion designated by the lower case letter is the quaternion designated by the upper case letter with an angle half the quaternion angle of the quaternion written in upper case.

The framed vector for the eye

For present purposes the location of the eyeball will be at the origin of the coordinate system. Therefore, the location vector it will be suppressed in the framed vector for the eyeball. The gaze direction, , will the first component of the framed vector for the eye. It is a special extension vector, a unit vector in the direction of the line of sight. The other extension vectors, , are generally unit vectors, where the radius of the eyeball is taken as unity. They enter into considerations of eye movements largely by indicating the insertions of the extrinsic eye muscles. The frame of reference for gaze, , is of prime importance in what follows.

Consequences of Donder’s law

The above expression is, in effect, Donder’s law. Given neutral gaze, it gives us the rule for calculating the orientation of the eyeball in any given eccentric gaze direction. Donder’s law is observationally verified for eye fixation, but one would presume that it would also apply during vestibulo-ocular, optokinetic, and smooth pursuit tracking movements, because vision is important during such eye movements. It has been demonstrated to apply during smooth pursuit (Haslwanter, Straumann et al. 1991). It need not apply during saccadic eye movements, because clear vision does not seem to be so important, although there are indications that we do see certain visual features during saccadic eye movements. For instance, it is possible to saccade to a target that is visible only during a previous saccade, which would imply that we maintain a well oriented map of the visual world even during saccades. Consequently, it is possible that Donder’s law is valid during all types of eye movements.

Since each gaze direction has a unique orientation associated with it and the placement of the eye is a function of the lengths of its muscles, it follows that the set of lengths of the extrinsic eye muscle must be a unique function of gaze direction. It should be possible to compute the length of each extrinsic eye muscle at each gaze direction. The set of the muscle lengths will form a surface that depends upon gaze direction. Donder’s law implies such a muscle length versus gaze direction surface exists. We will determine how such a surface can be computed (see below).

Donder’s law implies Listing’s plane

If one considers a few examples of gaze shifts from neutral gaze, then it becomes apparent that Donder’s law implies that the axes of rotation for all gaze shifts from neutral gaze lie in the coronal plane. For instance, if the eye moves medially or laterally then the vector of the rotation quaternion is vertical. If the eye moves up or down in the midline then the axes of rotation are directed medially and laterally and if the eye moves obliquely the axes of rotation are oblique and at right angles to the plane of the great circle trajectory. In general, the vectors of the quaternions of all great circle trajectories through a point lay in the plane that is perpendicular to the vector from the center of rotation to that point. The plane that contains the axes of rotation for all great circle eye movements from neutral gaze is called Listing’s plane. It is parallel to the coronal plane of the eyeball, because that plane is perpendicular to the line of sight. When used without qualification, this is the meaning of Listing’s plane. The existence of Listing’s plane implies that all the eye fixation movements are on great circle trajectories through neutral gaze.

Listing’s plane is a direct consequence of Donder’s law. Given a neutral gaze, , and an eccentric gaze direction, , one can compute the quaternion, , that rotates the neutral gaze into the eccentric gaze with the appropriate gaze orientation, .

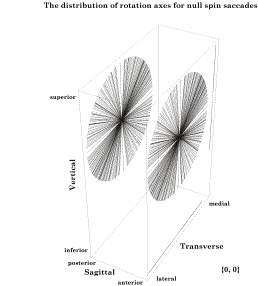
The axes of rotation for saccadic eye movements from neutral gaze to a wide range of eccentric gazes have been plotted with a common origin. Those axes are also shown projected upon the walls of a box aligned with the cardinal planes of the eye. Clearly all the axes lie in a plane that is aligned with the coronal plane of the eye. The plane that contains all of the axes of rotation is Listings plane for saccades from neutral gaze. [see (Langer 2005l) for details.]

Generalization of Listing’s plane to saccades between eccentric gazes

You may have noted that the statements in the last paragraph referred only to movements from neutral gaze. One might think that the shortest path between two gazes, that is the great circle through their gaze directions, is the best path for all eye movements. However, a little experimentation will quickly show that it is not. Unless the two eccentric gazes lie on a great circle that passes through neutral gaze, moving along a great circle trajectory will leave the eye rotated about its line of sight relative to the orientation predicted by Donder’s law. In other words, great circle trajectories between eccentric gazes introduce an additional concurrent twist to the gaze orientation. That additional twist with geodesic trajectories through points other than the reference point is a property of rotations in three-dimensional space and not peculiar to the eye. A natural question is - how does the nervous system deal with it? The answer takes us into some interesting mathematics. It also leads to a generalization of the meaning of Listing’s plane.

If one starts from an eccentric gaze and ends at another eccentric gaze, the quaternion for the movement that ensures that the orientation is correct at both gazes is the ratio of the frame of reference of the final gaze to the frame of reference of the initial gaze. That relationship was first noticed in the 1800’s and it is called Listing’s Law. The actual statement of Listing’s laws was in different language from that used here, but the current language is equivalent.

The axes of rotation for rotations from a particular gaze to all other gazes also lie in a single plane, which will also be called Listing’s plane. However, this more general Listing’s plane is different in several important ways from the traditional meaning for eye movements from neutral gaze. These differences arise from the axes of rotation being for conical rotations, rather than great circle rotations.

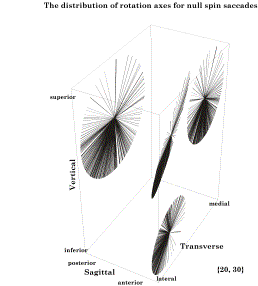
The axes of rotation for saccades from an eccentric gaze, 20° medial and 30° elevation, are plotted in the central disc and projected upon the walls of a box aligned with the cardinal planes of the eye. All the axes lie in a plane that is tilted 10° medially and 15° anteriorly. The plane of the axes of rotation is Listing’s plane for saccades to and from that eccentric gaze direction.

For reasons that will be developed below, one must redefine the relationship between gazes and the rotations that carry one from one to another. Listing’s law can be stated as follows. If the starting gaze is and the final gaze is , and both gazes satisfy Donder’s law, then the quaternion that turns into , without introducing additional torque is given by the ratio of their orientations.

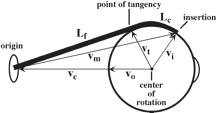
The other half of the law is that for a given initial or final gaze, all trajectories meeting this condition have a quaternion with a vector that lies in a single plane, which will also be called Listing’s plane.

For movements from neutral gaze, Listing’s plane is parallel to the equatorial plane of the eye when it is in neutral gaze. That is the usual meaning of Listing’s plane. For eccentric gazes, the plane containing the axes of rotation for the saccades is tilted relative to that equatorial plane by an angular excursion half the angular excursion from neutral line of sight to the eccentric line of sight. That plane is different from the usual Listing’s plane. It is not perpendicular to a vector from the center of rotation to the gaze direction. The axes of rotation are the vectors of quaternions for conical rotations. Consequently, the vectors in the plane are not perpendicular to either the starting gaze direction or the final gaze direction.

The name is retained because the usual Listing’s plane, for saccades from neutral gaze, is a special case of the generalized Listing’s plane, for saccades from eccentric gazes. The general form of Listings plane is different from that for neutral gaze in subtle ways, but it is necessary to develop a few additional concepts before the differences can be adequately described. Consequently, we will return to these concepts at the end of this chapter.

Donder’s and Listing’s laws quite marvelous and remarkable when expressed in this fashion, but they are even more elegant when one notes that both laws are logical consequences of the observation that eccentric gazes are the gazes obtained by following great circle trajectories from neutral gaze. Consequently, Listing’s Law is a logical consequence of Donder’s Law and Donder’s law is in effect a conservation law. Von Helmholz noted this quality of Donder’s law in the mid-1800’s. It was actually von Helmholz who formulated Donder’s law as we generally state it. The details of this relationship are developed elsewhere (Langer 2005l). We will return to consider these observations in greater detail, but it necessary to develop some additional concepts before doing so. We start by sorting out a method of describing eye movements and gaze in terms of muscle lengths.

The Muscle Length Surface

Let us now turn to the mechanical basis for these relationships. To do that, we need to compute the lengths of the extrinsic eye muscles when the gaze has any arbitrary direction in the physiological range of the eye’s movements. Computing the length of each muscle at each gaze direction is computationally possible by noting that the muscle takes the most direct path from its origin to its insertion, contingent upon its having to lie on the surface of the eyeball. If we know the center of rotation and the locations of the muscle’s origin and insertion, then it must lie in the plane of the quaternion that is the ratio of the vectors that point from the center of rotation to each attachment site. We note that the point of tangency occurs where a vector from the center of rotation to the muscle is perpendicular to the muscle. Because the segment of the muscle that extends from the origin to the point of tangency is constant, changes in muscle length are effectively due to changes in the length of muscle lying upon the eyeball, that is the variation in the angular excursion between the point of tangency and the point of insertion is the same as the variation in muscle length. For that reason, it is convenient to express changes in muscle length in degrees of angular excursion. Consequently, for present purposes, the differing resting lengths of the entire recti are of little consequence to the arguments. Muscle length is expressed as the change in length from its value in neutral gaze.

The length of an extrinsic eye muscle is the distance from its origin to its point of tangency with the eyeball plus the distance from the point of tangency to its insertion. Given the locations of the center of the eyeball, the muscle’s origin, and the muscle’s insertion, one can compute the quaternion of the plane that contains the origin, insertion and point of tangency and, therefore, compute the length of the muscle for any gaze.

Donder’s law effectively says that if we plot gaze orientation as a function of gaze direction, then the plotted points for muscle length will form a surface in an eight dimensional space, two dimensions for gaze direction and six for the lengths of the six extrinsic eye muscles. For every combination of location coordinates, there is a unique orientation. This means that, for each gaze position, there is a unique set of extrinsic eye muscle lengths.

As just illustrated, we can compute the muscle lengths for each muscle at each gaze by measuring the distance from the muscle’s origin to its insertion when the eye has that gaze. The result is that, for each muscle, there is a surface in a three-dimensional space (gaze direction and muscle length) and if we plot the surface for each muscle then we obtain a surface much like that in the following figure. The surface does not look like a surface, because we have collapsed all the individual muscle length axes on to a single axis, but it is in fact a single surface.

The separate surfaces in the plot are comparable to the contour lines on a topographic map that indicate elevation in the third dimension, which has been collapsed into the plane of the map. In some ways this representation is more useful in that one can read off the muscle length of each muscle at a particular gaze direction. The component surfaces are mildly curvilinear and tilted with respect to gaze direction. For instance, the lateral rectus becomes longer as the eye moves medially and the inferior rectus becomes longer as the eye looks up. The curvature of the surfaces indicates that the interactions between the muscles are not linear, but also not grossly non-linear.

Muscle lengths are plotted versus gaze direction for each of the six extrinsic eye muscles. Length is measured relative to the length in neutral gaze and expressed as degrees of angular excursion of the eye. All the muscle length axes have been collapsed upon a single axis, therefore the surface does not look like a surface, but like six surfaces. The initials indicate which surface component is associated with each muscle.

The illustrated surface was computed assuming that there are fascial slings constraining the muscles. The surface is subtly different if one does not assume the constraints of the fibromuscular slings (Langer 2005j; Langer 2005k).

The muscle length surface was first computed assuming the simple organization typically presented in most textbooks where the muscle pull directly from their origins to their insertions (Langer 2005j) and then for a more realistic model in which the muscles pass through a suspensory membrane that contains thickened fascial slings that provide fulcra for the muscle, thus provide rather different effective origins. The muscle length surface is only moderately changed by introducing the fascial slings. In general the component surfaces are flattened and more aligned with the medial/lateral and superior/inferior axes of the orbit. The above plot is based on the more realistic model with fascial slings (Langer 2005k). The model chosen will also affect some of the other parameters computed, such as pulling directions for the individual muscles and the degree of spin and swing imparted to the eyeball at a given gaze (see below).

For each gaze direction, one can obtain the muscle lengths by passing a perpendicular to the plane of gaze directions and reading off where it intersects the surface. One might speculate that this surface is learned by the nervous system and expressed as a neural network of connections that translate a desired gaze direction into a set of motor neuron activities. The nervous system need only send the desired gaze into the network and the appropriate combination of muscle contractions are produced by a pattern generator in the brainstem reticular formation.

Assuming that circuitry exists that somehow converts a gaze direction into an appropriate set of muscle lengths, this concept gives a relatively simple means of ensuring that when the eye reaches a particular gaze direction, it will have the correct gaze orientation. As an eye movement carries the line of sight across the visual field one is guaranteed an optimal orientation of the visual image upon the retina because it moves through the muscle length surface. For fixation and smooth tracking eye movements, the muscle length surface provides a parsimonious solution to the generation of correctly oriented gaze in all gaze directions.

Pulling Directions

It is conventional to characterize the extrinsic eye muscles in terms of their actions. For instance, the lateral rectus abducts the eye and the superior rectus elevates it. The implicit assumption is that the nervous system uses these labels to produce eye movements. The eye muscle length surface introduced above is a more parsimonious hypothesis, but, leaving that aside, do the eye muscles have a consistent action? Computing the pulling directions of the extrinsic eye muscles at eccentric gazes is actually a fairly difficult computational problem, normally. However, the quaternion model developed for the calculations described above provides the pulling directions as a direct result of the description of the anatomy of the eyeball.

It turns out that the pulling directions of the recti are fairly consistent at most eye positions. That is especially true if the fascial slings in the suspensory membrane are incorporated in the model. The oblique eye muscles are different. With some gazes, they function largely as torsion generators and in other directions they function largely as elevators and depressors. They are effective elevators and depressors when the eye is looking medially and effective intorters and extorters when the eye is looking laterally.

When the eye is looking laterally, the superior oblique muscle pulls it down and further laterally. Note however, that the arrows are shorter on the lateral side of neutral gaze. Since the muscle shortening is the same for all of the gaze directions, the relative shortening of the pulling direction arrows indicates that the muscle is also causing a substantial amount of rotation about the axis of rotation for the muscle.

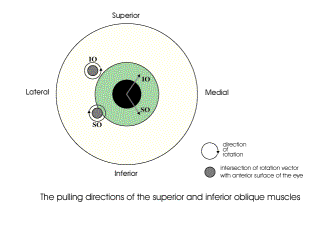
For each gaze direction in a grid 90° on a side and centered on neutral gaze, the pulling direction and excursion of a constant small shortening of the superior oblique muscle was computed. The green disc indicates the normal range of eye movements. We can probably look close to 45° laterally, so it may be a bit conservative.

The arrows indicate the direction and magnitude of the pull for the gaze direction located at the origin of the vector. For the superior oblique muscle the pulling direction and magnitude are clearly functions of gaze direction. For medial gaze, much of the muscle shortening goes into changing gaze direction by depressing the eye. In lateral gaze, only a fraction of the shortening results in changing gaze direction, pulling gaze down and lateral. The rest is involved in changing the orientation of the eye.

The axis of rotation is the vector of the quaternion for the plane that defines the axis of the muscle. In the case of the superior oblique muscle, the tendon as it extends from the trochlea to the insertion on the posterior lateral surface of the eyeball defines the plane of rotation. If we extend that vector from the center of rotation through the anterior aspect of the eyeball, then it exits a short distance lateral and below the pupil, when the eye is looking straightforward. Given the pulling direction of the superior oblique, that means that the muscle tends to pull the line of sight down and medially when the eye is in neutral position. It is a bit confusing, because the muscle pulls gaze down and lateral, but the effect is to move the eye down and medial. The reason is that the axis of rotation is below and lateral to the line of sight. The same type of calculation indicates that the inferior oblique pulls the line of sight up and medial. It should be pointed out that comparatively small changes in the placement of the insertion of these muscles can have large consequences for their actions.

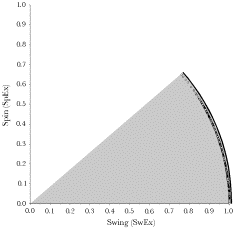
The oblique muscles pull the eye in a diagonal direction that involves both spin and swing. In this figure the intersection of the axes of rotation with the anterior aspect of the eyeball when in neutral gaze are plotted on the eyeball along with their directions of spin. Because of the eccentric location of the axes of rotation and the directions of their spin components, the effect of contraction of the superior oblique is to move gaze down and medially. The effect of the inferior oblique is to pull the eye up and medial.

One of the puzzling findings from computing the pulling directions of the eye muscles is that at quite eccentric positions, the eye muscles, as a group, tend to become less effective at bringing the eye back towards neutral gaze. All the muscles pull the eye away from neutral gaze. However, some thought reveals that that is not a problem, because eccentric eye movements passively distort the suspensory membrane and it will act as a restoring spring that pulls the eye back towards neutral position. That is seen to be the case in dead persons, where the eyes come to rest approximately in neutral position.

By computing the pulling directions in a situation in which the fascial slings in the suspensory membrane are not part of the anatomical description and a situation in which they are, it may be seen that the slings render the pulling directions of the extrinsic eye muscles more consistent. Essentially they remove the medial placement of the annulus of Zinn as a consideration. Without the suspensory membrane the superior and inferior recti pull medially as well as elevate and depress the eye. If the eye is looking laterally about 22°, then they become pure elevators and depressors. With the suspensory membrane they are consistent elevators and depressors over the full range of medial and lateral gazes.

It is argued here that while pulling directions are a convenient way to remember and test the actions of the eye muscles, it is the net effect of all the muscles working together that determines gaze. In the absence of one or more eye muscles, the other muscles partially compensate. For instance, following the loss of the abducens nerve, the eye can be brought to neutral gaze by suitable adjustments of the other muscles. It is when the individual tries to look laterally that the gaze is greatly distorted.

Spin and Swing

When considering the pulling directions of the superior oblique, it was noted that the same amount of muscle shortening causes more or less movement of the line of sight. That is because a rotation may be viewed as involving more or less spin or swing, depending on the frame of reference. In the case of the eye, the logical frame of reference is the line of sight and the vertical and horizontal meridians. Contraction of a muscle will move the globe a distance in a particular direction, but part of that movement will cause the line of sight to move and part will cause the eye to rotate about its line of sight. For instance, if the force is applied to the equator in a direction parallel with the equator, then the rotation will be pure swing at the equator, pure spin at the North Pole, and a mixture of both at all other latitudes. In this instance, we measure the muscle contraction as an angular excursion, say 5°. In the plane of the muscle, the eye moves through 5° of pure swing. Where the axis of rotation intersects the surface of the eye, the movement is 5° of pure spin. However, the point of reference for movements of the eye is the effect that they have on the visual field projection on the retina. In that frame of reference, the movement is a combination of an angular excursion of the line of sight, that is, a change in gaze direction, and a rotation about the line of sight, that is, a change in gaze orientation.

The first of these movement components corresponds to swing and the second corresponds to spin. Since both are angular excursions and we are more interested in the relative amounts of each than in the absolute amounts, it is convenient to divide both by the total angular excursion of the muscle contraction. In that case we are talking about spin over angular excursion, which will be symbolized by SpEx, and swing over angular excursion, which will be written as SwEx.

The movement is computed by rotating the eye, represented by a framed vector, through a standard size angular excursion about the vector of the muscle quaternion for a particular gaze. The new gaze is compared to the initial gaze by taking the ratio of the lines of sight in the two gazes to obtain the swing and then computing the rotation that rotates the gaze orientations aligned about their directions of gaze so as to bring the other two axes into alignment to obtain the spin component. In other words we take the ratio of the two frames using the line of sight as the basis of the first quaternion. The angle of the first quaternion is the swing and the angle of the second quaternion is the spin. When we perform this calculation, it is always found that the individual components are smaller than or equal to the total excursion.

When the movement is a pure spin or a pure swing, then the component is equal to the total angular excursion. Otherwise, each component is less than the total excursion. On the other hand the total excursion is less than, or equal to, the sum of the two components. If we plot the swing component versus the spin coordinate for a great many examples, as in the following figure, then they form an arc between the spin axis and the swing axis. The arc appears to be circular, but it is not quite a circle. The solid line is an arc of a circle with a radius of 1.0. Still, to a fairly good approximation, the following relationship holds between spin and swing in most situations.

Change in gaze is divided into a component that changes gaze direction (SwEx) and a component that changes gaze orientation (SpEx). Each of these may be expressed as an angular excursion. Each of these components is less than or equal to the movement, but the sum of the two component angular excursions is greater than the total movement excursion. The relationship between the components and the total movement (the data points) is well approximated by a circle (solid curved line).

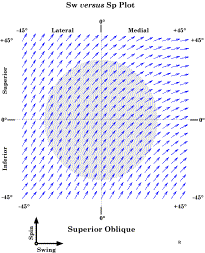
The change of gaze following a small shortening of the superior oblique muscle is divided between the change in gaze direction (SwEx) and the change in gaze orientation (SpEx). These changes correspond to swing and spin, respectively. When we plot the relative amounts of swing and spin for each gaze direction, there is a substantial fraction of each at all gaze directions when examining the pulling directions of the superior oblique muscle.

If we plot the relative amounts of SpEx and SwEx for each gaze direction with contraction of the superior oblique muscle as components of a vector, as is done in the following figure, then we can readily see that there are substantial amounts of both in all physiological gaze directions. If the effect of a muscle is to pull the eye in a direction aligned with a great circle through the direction of neutral gaze, then the vectors are aligned with the swing axis, so they are horizontal in the plot. If the muscle causes the eye to spin about the line of sight, then the vector will be vertical in such a plot. The recti tend to have SpEx versus SwEx plots with all the vectors nearly horizontal. The plots for both oblique muscles have most of their vectors closer to a 45° angle, meaning comparable amounts of spin and swing.

Saccades between eccentric gazes

The problem

Rotations in three dimensions have some unexpected consequences. In particular, if one makes a saccade from a gaze directed up and laterally to a gaze direction directed up and medially, the shortest path would be a great circle trajectory that joins the two gaze directions. Unfortunately, such a trajectory will leave the eyeball rotated relative to the orientation it should have according to Donder’s law. There will be an additional twist to the orientation, beyond the shift mandated for that gaze direction.

While the discrepancy is often small, there must be some sort of compensation in order for the movement to be successful. A series of such misaligned eye movements could leave the eye significantly twisted relative to the correct orientation. It is readily observed that such misalignments do not occur. Therefore, the nervous system must not use geodesic trajectories in these circumstances.

There are many possible solutions. For instance, there might be a compensatory twist during the movement. However, these types of solution are unsatisfactory, unless one has a mechanism that will guarantee the correct amount of twist to ensure the correct outcome. All in all, it is improbable that geodesic trajectories are an efficient or likely means of moving from one eccentric gaze to another, even though great circle trajectories work well for eye movements from neutral gaze.

Another solution might be to control the muscle lengths with a feedback circuit. However, the timing of saccades is too fast for such a circuit to operate and saccades seem to be pre-packaged ballistic movements. So, although the programming of the saccade must be about the flow of activity to the extrinsic muscles, it does not appear to be a feedback circuit that drives the eye to its new gaze and ensures that it has the correct orientation. Whatever happens to program the saccade must happen in the central nervous system.

It is possible that the muscle length surface codes the transformation from a proposed gaze to its realization in a set of muscle activities. In fact it will be argued that such a system might well be the means by which the null spin trajectories are generated. Clearly, the central nervous system does not compute quaternions, so, there must be a physiological mechanism that produces the appropriate behavior. The circuits responsible for the muscle length surface may be the mechanism used. However, even if they are, that does not ‘explain’ the nature of the solution or why it is the solution. The following considers a formal solution that leads us to a possible physiological solution.

A possible solution

The problem of having to introduce a compensatory twist to the movement might be avoided by following a trajectory that automatically compensates for the torsion of the eye. However, we have to determine if such trajectories exist and, if they do, figure out a way to compute them that makes physiological sense. Then, we have to experimentally determine if such trajectories are likely to be the solution that the brain has chosen.

In fact, such trajectories do exist, they are easily computed with the tools introduced here, there is a possible physiological means of automatically generating them, and they appear to be the solution that the nervous system has chosen to use.

Saccades and saccades

To simplify discussion, the term saccade is used in an unconventional manner in the following. A saccade will be a unitary circular movement that may be described as a conical rotation. Note that circular movements may not look very circular on the surface of a sphere. After all great circles appear to be straight lines on the surface of a sphere.

Real saccades are far more irregular and they involve burst and tonic components. They may not be consistent from saccade to saccade, unless practiced. They have many dynamic features that we will not consider here.

The justification for using this nomenclature is that many of the features that will be deduced for these ideal saccades will turn out to be properties of actual saccades. An accurate descriptive nomenclature for these idealized movements, such as, unitary conical rotations about a prescribed axis of rotation, rapidly becomes very cumbersome with repetition, so, we need a shorthand. Saccade has the right connotation and it is brief. In general, the idealized eye movement type of saccade will be italicized for clarity.

Null spin trajectories

Saccades that carry the eye along a smooth circular trajectory from a starting gaze to a final gaze with automatic compensation for torsion are not generally great circle trajectories. They follow great circles if and only if they are saccades to or from neutral gaze. Otherwise, they are conical rotations and they may be computed by taking the ratio of the gaze orientation at the final gaze direction to the gaze orientation at the initial gaze direction. We know that both gazes must have null spin relative to neutral gaze, because of Donder’s Law. Consequently, one need only compute the orientations for great circle trajectories from neutral gaze to each gaze direction and then take the ratio of the two orientations to obtain the quaternion that specifies the conical rotation that carries the initial gaze into the final gaze with precisely the spin needed to end in the proper orientation for that gaze direction.

Given the two eccentric gazes and , the quaternions that rotate neutral gaze into each eccentric gaze are as follows.

The starting and final gazes may then be computed.

The quaternion that rotates the initial gaze into the final gaze is then the ratio of the orientations of the gazes.

Computing trajectories

One can compute the null spin trajectory of the saccade by substituting a series of angular excursions as the angle of the quaternion in the last equation.

One can also obtain the quaternion for the great circle trajectory by taking the ratio of the direction of the final gaze to the direction of the initial gaze and then multiplying the initial gaze by the great circle quaternion with a series of different angular excursions.

How different are null spin saccades and great circle saccades?

These calculations have been done for a variety of starting and ending gaze positions (Langer 2005l). It turns out that there is comparatively little difference between the great circle trajectories and the null spin trajectories, unless one is jumping between two far separated eccentric gaze directions. The following figure illustrates the geodesic and conical rotation trajectories for saccades from a far eccentric gaze to a wide range of other gazes. It is necessary to choose a very eccentric gaze in order to clearly see that the null spin and great circle trajectories are in fact different. The greatest discrepancies occur when the starting and ending gazes are both far eccentric and the trajectory does not pass near neutral gaze. The two trajectories are identical if the gazes lie on opposite sides of neutral gaze, when the null spin trajectory is the great circle trajectory.

The shortest path between two gazes (Great Circle) and the path with null spin (Null Spin) have been computed for a collection of saccades that start at 30° of lateral rotation and 30° of elevation and move to a gazes at an array of gaze directions. The differences between the two trajectories are generally small and the differences in saccade length are quite small. The eccentric gaze was chosen to make the differences as large as possible within a physiologically possible range of gazes. In practice, we almost never make single saccades as large as the longer saccades represented here.

For saccadic eye movements, where clear sight is not a premium, it might be possible to jump off the muscle length surface and cross the intervening space, in a sense taking a shorter path. From the last chapter, we know that the saccades that follow the shortest path between two gaze directions will not be correctly oriented when it arrives at its final gaze direction, because the final position will not be null spin relative to neutral gaze. The slightly longer null spin saccades that are the ratio of the final gaze orientation to the initial gaze orientation will be correctly aligned. If one calculates of two trajectories, the one in the muscle length surface versus the shortest path between the gaze directions, the differences are not great, perhaps not distinguishable in most experimental preparations (Langer 2005l).

It also happens that all the rotation vectors of the saccades will lie in the same plane, which will be tilted relative to the coronal plane by an amount half the eccentric gaze direction offset. The axes of rotation for the geodesic saccades will also lie in a single plane, but it will be orthogonal to the direction of the eccentric gaze. It has been observed that the rotation axes of actual saccadic eye movements have their axes of rotation in a generalized Listing’s plane tilted half way to the eccentric gaze direction (Tweed and Vilis 1988; Tweed and Vilis 1990). We will now show that such saccades would flow in the muscle length surface.

Null Spin Saccades

Null spin defined

In conclusion, let us consider a bit more complex concept. All eye movements away from neutral gaze will change the orientation of the eye. However, those that follow geodesic trajectories away from neutral gaze will rotate just enough and in the correct directions to keep the visual image optimally oriented upon the retina. Because great circle trajectories do not introduce spin from the point of view of the moving object, such saccades will be said to be null spin saccades. The resulting gazes will be said to be spin neutral gazes. Consequently, Donder’s law says that all natural gazes are spin neutral gazes.

Null spin is not transferable by congruence

It was illustrated in the last chapter that null spin is not a property that can be transferred by a congruence operation. So, if means that A has null spin relative to B, then

In general, if two eccentric gazes () are both spin null relative to neutral gaze (), then it is generally not the case that

.

That is why the great circle trajectory from a to b does not yield the correct final gaze.

We have just outlined a method that will always yield the conical rotation that will rotate into .

What is more, if we calculate the value of the gaze for each point along the trajectory described by this expression and compare it with the spin null gaze for the same gaze direction, then it is found that the two gazes are identical. Every gaze along the trajectory is spin null relative to neutral gaze. All gazes in a spin null saccade are spin neutral gazes. Consequently, conical rotation yields exactly the set of gazes that are prescribed by Donder’s law.

This means that every gaze in a null spin saccade is on the muscle length surface that was calculated for visual fixation gaze directions. Therefore, if one assumes a system that uses the approach laid out here to find the saccades between eccentric gazes, which seems to be the case for the human oculomotor system, then the saccades travel in the muscle length surface that was derived for visual fixation and smooth eye movements. Conversely, the saccade may be coded by feeding a signal through the same brainstem pattern generators as were used for smooth eye movements with suitable adjustments for the burst component of the saccade.

The relation between the conical rotations that have their vectors in the generalized Listing’s plane for an eccentric gaze and null spin saccades is extremely elegant. Even though the gazes along the trajectory are not null spin relative to each other, they produce precisely the amount of rotation necessary to render the gazes along the trajectory null spin relative neutral gaze. The set of null spin saccades is the set of trajectories that solve the problem of concurrent twisting of the gaze orientation to match the gaze direction. They lie in the muscle length surface, therefore the surface provides a means of obtaining the correct eye movements without having to actually compute the quaternions for the conical rotations.

Since the actual rotation quaternion for a particular saccade is the intersection of the generalized Listing’s planes for its initial gaze and for its final gaze, the appropriate saccade may well flow directly form the brainstem eye movement generators by inputting the current gaze direction and the desired gaze direction.

In Summary

The eye is a good model system to study anatomical movements, because of the relatively simple anatomy. However, if you consult the papers dealing with the details of the points considered here (Langer 2005j; Langer 2005k; Langer 2005l), you will find that the equations describing the anatomy are rather complex and the calculations are complex enough to require a reasonably fast computer to obtain results in a timely fashion. Those papers also consider a wider range of topics and examples than is feasible to consider here.

The eye allows us to see how a system of muscles might control the actions of a joint or joints. One of the striking observations that one makes when carrying out an analysis on even this simple system is that it is incredibly complex. Just the geometry can be daunting, but if one considers that muscles interact in a highly non-linear fashion that depends complexly upon tension and length of many muscle elements, then it is clear that any control system for anatomical movements must be in the nature of a neural network, which learns by acting. There is no way that one could write down a set of analytical equations that can express what even a simple system does and yet the task is handled by a relatively small number of neurons in a few nuclei in the central nervous system. In this analysis, it was possible to sweep most of the difficulties of motor control behind a curtain, by considering only the movements and the muscle lengths and not how a system of interacting nonlinear elements finds a solution. Each muscle’s length and direction depends not only on the forces it generates, but also upon the forces in the other muscles and their lengths and directions. In the eye, there is a comparative lack of inertia and viscosity and there is constant loading, all of which are not true of most other joints. This analysis will not consider any of these problems. Still, it is well to remember that they are part of the problem for the nervous system. Even this level of analysis suggests how motor control might function, by showing how anatomical movement operates and perhaps providing tools for its description and manipulation.

Clark, R. A., S. J. Isenberg, et al. (1999). "Posterior fixation sutures: a revised mechanical explanation for the fadenoperation based on rectus extraocular muscle pulleys." Am J Ophthalmol 128(6): 702-14.

Clark, R. A., J. M. Miller, et al. (1997). "Location and stability of rectus muscle pulleys. Muscle paths as a function of gaze." Invest Ophthalmol Vis Sci 38(1): 227-40.

Clark, R. A., J. M. Miller, et al. (1998). "Displacement of the medial rectus pulley in superior oblique palsy." Invest Ophthalmol Vis Sci 39(1): 207-12.

Clark, R. A., J. M. Miller, et al. (2000). "Three-dimensional location of human rectus pulleys by path inflections in secondary gaze positions." Invest Ophthalmol Vis Sci 41(12): 3787-97.

Clark, R. A., J. M. Miller, et al. (1998). "Heterotopic muscle pulleys or oblique muscle dysfunction?" J Aapos 2(1): 17-25.

Clark, R. A., A. L. Rosenbaum, et al. (1999). "Magnetic resonance imaging after surgical transposition defines the anteroposterior location of the rectus muscle pulleys." J Aapos 3(1): 9-14.

Cogan, D. C. (1956). Neurology of the Ocular Muscles. Springfield, Ill., Charles C. Thomas.

Cogan, D. C. (1966). Neurology of the Visual System. Springfield, Ill., Charles C. Thomas.

Cogan, D. C. (1980). Neurology of Extraocular Muscles. Springfield, Ill., Charles C. Thomas.

Demer, J. L., J. M. Miller, et al. (1996). "Surgical implications of the rectus extraocular muscle pulleys." J Pediatr Ophthalmol Strabismus 33(4): 208-18.

Demer, J. L., J. M. Miller, et al. (1995). "Evidence for fibromuscular pulleys of the recti extraocular muscles." Invest Ophthalmol Vis Sci 36(6): 1125-36.

Demer, J. L., S. Y. Oh, et al. (2000). "Evidence for active control of rectus extraocular muscle pulleys." Invest Ophthalmol Vis Sci 41(6): 1280-90.

Demer, J. L., V. Poukens, et al. (1997). "Innervation of extraocular pulley smooth muscle in monkeys and humans." Invest Ophthalmol Vis Sci 38(9): 1774-85.

Haslwanter, t., D. Straumann, et al. (1991). "Smooth pursuit eye movements obey Listing's law in the monkey." Exp. Brain Res. 87(2): 470-472.

Langer, T. P. (2005j). Analysis of an Universal Joint: Movements and Muscles of the Eye.: http://homepage.mac.com/tlanger_sasktel_net/EyeMovements/eyemovements.html.

Langer, T. P. (2005k). Geometrical Anatomy of the Eye and Eye Movements In a Model with Restricted Extraocular Muscles.: http://homepage.mac.com/tlanger_sasktel_net/EyeMovements/eyemovements.html.

Langer, T. P. (2005l). The Static Gaze Surface and Null Spin Saccades: Spin Neutrality and Saccadic Trajectories.: http://homepage.mac.com/tlanger_sasktel_net/EyeMovements/eyemovements.html.

Leigh, R. I. and D. S. Zee (1991). The Neurology of Eye Movements. Philadelphia, F.A. Davis.

Standring, S. (2005). Gray's Anatomy. The Anatomical Basis of Clinical Practice. Edinburgh, Elsevier Churchill Livingstone.

Thurtell, M. J., M. Kunin, et al. (2000). "Role of muscle pulleys in producing eye position-dependence in the angular vestibuloocular reflex: a model-based study." J Neurophysiol 84(2): 639-50.

Tweed, D., H. Misslisch, et al. (1994). "Testing models of the oculomotor velocity-to-position transformation." J Neurophysiol 72(3): 1425-9.

Tweed, D. and T. Vilis (1987). "Implications of rotational kinematics for the oculomotor system in three dimensions." J Neurophysiol 58(4): 832-49.

Tweed, D. and T. Vilis (1988). "Rotation axes of saccades." Ann N Y Acad Sci 545: 128-39.

Tweed, D. and T. Vilis (1990). "Geometric relations of eye position and velocity vectors during saccades." Vision Res 30(1): 111-27.

Williams, P. L., L. H. Bannister, et al. (1995). Gray's Anatomy. The Anatomical Basis of Medicine and Surgery. New York, Churchill Livingstone.