Geometrical Anatomy of Joint Movement

My current research is involved with the description of anatomical movements with the formalism of quaternion analysis. Quaternions offer opportunities of greatly simplifying the description of anatomical movement by describing the anatomy and axes of rotation in an intuitive mathematical symbolism that allows one to readily calculate the consequences of movement in the described anatomy. Despite the simplification that this approach, or perhaps because of it, one often finds that anatomical movement has unexpected subtleties.

A generalized three-dimensional analysis of joint movement requires a powerful language that describes the anatomy of the joint in such a way as to allow one to compute the consequences of the anatomical configuration. Quaternions, an extension of complex numbers discovered by Sir William Rowan Hamilton, are just the language for such analysis. Their characteristics exactly model the nonlinear properties of rotations in three dimensional space. Once one has created a mathematical structure that encapsulates the location, extension, and orientation of anatomical objects such as bones and joints, here called framed vectors, then one can apply quaternion analysis to the calculation of the consequences of anatomical movements in the described joints. In the last few years, I have applied these methods to the analysis of movements of the eyeball in the orbit, the movements of the atlanto-axial joint and the manner in which the vertebral artery is stressed across that cervical joint, the movements of the lower cervical spine, movements of the lumbar spine, and analysis of the semicircular canal. Online descriptions of many of these observations may be found in the personal webpage listed below.

This approach to the analysis of joint movement allows one to describe the joint in what appears to be an anatomically valid manner and then ask what the implications are for movement in the joint. For instance we can describe the eyeball, the muscle attachments of the extrinsic eye muscles, and the manner in which they lie relative to the orbit. Then calculation allows one to study the manner in which the muscles move the eye when it is in any anatomical position and orientation. These calculations have been performed with the standard model, generally taught in anatomy and physiology courses, and the actual anatomy that contains fascial slings and partitions. It was found that the actual anatomy linearizes the muscle actions, so that the extrinsic eye muscles pull more consistently in the cardinal directions.

This approach leads to a natural description of the permitted gaze directions and orientations as a two dimensional muscle length surface in an eight dimensional space (six muscles and two angular directions of displacement for the line of sight). In a separate analysis it was discovered that, even though it is not logically necessary, saccade trajectories probably travel in or near that surface. Consequently, the same neural control system will suffice for computing the muscle lengths for saccades, smooth pursuit, compensatory vestibular eye movements, and visual fixation. As a result, torque of the visual field will not be introduced by eccentric eye movements.

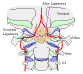Studies of the atlanto-axial joint were able to explain why the premanipulative hold for rotatory manipulation of that joint was observed to be the most stressful movement for that joint in the sense that, in normal subjects, more that half will experience occlusion of the vertebral artery on the side opposite the direction of rotation. The reason lies in the anatomy of the joint and, particularly, the manner in which the alar ligaments are attached.

The lower cervical spine defies analysis in terms of cardinal directions because the two axes of rotation are not orthogonal and the sideflexion/lateral rotation axis is has different obliquity for each vertebral joint. The quaternion analysis of framed vectors is no more difficult to compute for non-orthogonal axes than it is for orthogonal axes and it naturally expresses the consequences of concatenated joints. Therefore, the analysis was able to express the nature of movements in such system and how they combine non-linearly to produce the elegant movements that we observe in actual necks. These studies also brought new understanding of how the frame of reference for observations may profoundly affect what one observes.

Current studies involve casting the analysis of strain into a similar formulation and early considerations of the anatomy of the scapular and humeral joints.

Recent Publications

Arnold, C, R. Bourassa, T. Langer, and G. Stoneham (2003) Doppler studies evaluating the effect of a physical therapy screening protocol on vertebral artery blood flow, Manual Therapy, 9/1: 13-21. [http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?CMD=Display&DB=pubmed]

See personal webpage for online publications